题目内容
14.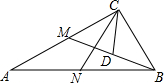 已知,在Rt△ABC中,∠ACB=90°,∠A=30°,点M、N分别是边AC、AB的中点,点D是线段BM的中点.
已知,在Rt△ABC中,∠ACB=90°,∠A=30°,点M、N分别是边AC、AB的中点,点D是线段BM的中点.(1)求证:$\frac{CN}{AB}=\frac{CD}{MB}$;
(2)求∠NCD的余切值.
分析 (1)根据直角三角形的性质即可得到结论;
(2)过M作MN⊥AB于H,由直角三角形的性质得到CN=AN=$\frac{1}{2}$AB,由等腰三角形的性质得到∠ACN=∠A=30°,解直角三角形即可得到结论.
解答 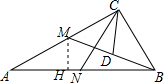 解:(1)∵在Rt△ABC中,∠ACB=90°,点N分别是边AB的中点,点D是线段BM的中点,
解:(1)∵在Rt△ABC中,∠ACB=90°,点N分别是边AB的中点,点D是线段BM的中点,
∴$\frac{CN}{AB}$=$\frac{1}{2}$,$\frac{CD}{MB}$=$\frac{1}{2}$,
∴$\frac{CN}{AB}=\frac{CD}{MB}$;
(2)过M作MN⊥AB于H,
∵点N分别是边AB的中点,
∴CN=AN=$\frac{1}{2}$AB,
∴∠ACN=∠A=30°,
∴∠NCD=∠MCD-30°=∠CMB-30°=∠MBA,
∴设BC=2k,则MA=$\sqrt{3}$k,MH=$\frac{\sqrt{3}}{2}$k,HB=4k-$\frac{3}{2}$k=$\frac{5}{2}$k,
∴cos∠NCD=$\frac{HB}{MH}$=$\frac{\frac{5}{2}k}{\frac{\sqrt{3}}{2}k}$=$\frac{5\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定和性质,解直角三角形,直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.人体中一种细胞的形状可以看成是圆形,它的直径为0.00000156米,这个数用科学记数法表示是( )
| A. | 156×10-8 | B. | 15.6×10-7 | C. | 1.56×10-5 | D. | 1.56×10-6 |
2.下列一元二次方程中,有两个相等实数根的是( )
| A. | x2-8=0 | B. | 2x2-4x+3=0 | C. | 9x2-6x+1=0 | D. | 5x+2=3x2 |
19.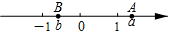 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
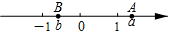 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )| A. | ab>0 | B. | a+b>0 | C. | (a-1)(b-1)>0 | D. | (a+1)(b-1)>0 |
6.计算(-12)÷4的结果是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
3.据统计,2015年湖南省旅游总收入3713亿元,把3713亿这个数字用科学记数法表示为( )
| A. | 3713×l08 | B. | 3.713×1010 | C. | 3.713×1011 | D. | 3.713×1012 |
4.已知m=8-$\sqrt{20}$,估算m的值所在的范围是( )
| A. | 1<m<2 | B. | 2<m<3 | C. | 3<m<4 | D. | 4<m<5 |
 己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题:
己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题: