题目内容
8. 已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知:如图,在△ABC中,CB=CA,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.(1)求证:DE是⊙O的切线;
(2)若BD=1,cosB=$\frac{1}{2}$,求$\widehat{DB}$的长.
分析 (1)连接OD、CD,如图,利用圆周角定理得到∠BDC=90°,则CD⊥AB,再利用等腰三角形的性质得AD=BD,于是可判断OD为△CAB的中位线,所以OD∥CA,然后证明DE⊥AC,于是利用切线的判定定理可得到结论;
(2)利用特殊角的三角函数值得到∠B=60°,则△OBD为等边三角形,所以∠BOD=60°,BD=OB=1,然后根据弧长公式求解.
解答 (1)证明:连接OD、CD,如图,
∵CD为直径,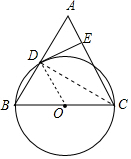
∴∠BDC=90°,
∴CD⊥AB,
∵CB=CA,
∴AD=BD,
而BO=CO,
∴OD为△CAB的中位线,
∴OD∥CA,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵cosB=$\frac{1}{2}$,
∴∠B=60°,
而OB=OD,
∴△OBD为等边三角形,
∴∠BOD=60°,BD=OB=1,
∴$\widehat{DB}$的长=$\frac{60•π•1}{180}$=$\frac{π}{3}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了弧长公式和等腰三角形的性质.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
19.下列计算正确的是( )
| A. | x3+x3=x6 | B. | (ab4)2=ab8 | C. | (m5)5=m10 | D. | x3y3=(xy)3 |
3.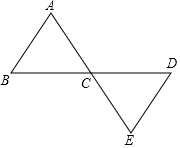 如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
 如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动. 当微型机器人移动了2016cm后,它停在了点A上.
13.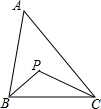 已知P为△ABC三边垂直平分线的交点,且∠BAC=40°,则∠BPC=( )
已知P为△ABC三边垂直平分线的交点,且∠BAC=40°,则∠BPC=( )
 已知P为△ABC三边垂直平分线的交点,且∠BAC=40°,则∠BPC=( )
已知P为△ABC三边垂直平分线的交点,且∠BAC=40°,则∠BPC=( )| A. | 70° | B. | 80° | C. | 120° | D. | 110° |
17.合肥市2017年中考的理化生实验操作考试已经顺利结束了,绝大部分同学都取得了满分成绩,某校对九年级20个班级的实验操作考试平均分x进行了分组统计,结果如下表所示:
(1)求a的值;
(2)若用扇形统计图来描述,求第三小组对应的扇形的圆心角度数;
(3)把在第二小组内的两个班分别记为:A1,A2,在第五小组内的三个班分别记为:B1,B2,B3,从第二小组和第五小组总共5个班级中随机抽取2个班级进行“你对中考实验操作考试的看法”的问卷调查,求第二小组至少有1个班级被选中的概率.
| 组号 | 分组 | 频数 |
| 一 | 9.6≤x<9.7 | 1 |
| 二 | 9.7≤x<9.8 | 2 |
| 三 | 9.8≤x<9.9 | a |
| 四 | 9.9≤x<10 | 8 |
| 五 | x=10 | 3 |
(2)若用扇形统计图来描述,求第三小组对应的扇形的圆心角度数;
(3)把在第二小组内的两个班分别记为:A1,A2,在第五小组内的三个班分别记为:B1,B2,B3,从第二小组和第五小组总共5个班级中随机抽取2个班级进行“你对中考实验操作考试的看法”的问卷调查,求第二小组至少有1个班级被选中的概率.