题目内容
7. 如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.
如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.(1)当t为2s时,△BEF为等腰直角三角形;
(2)当t为3s时,△DFC为等腰直角三角形;
(3)是否存在某一时刻,使△EFB∽△FDC?若存在,求出t的值,若不存在,请说明理由.
分析 (1)由已知条件易证四边形ABCD是矩形,所以∠A=∠B=∠C=90°,若△BEF为等腰直角三角形,则BE=BF,进而可求出t的值;
(2)由(1)可知∠C=90°,若△DFC为等腰直角三角形,则CF=DC,进而可求出t的值;
(3)若△EFB∽△FDC,则BE:CF=BF:DC,结合题目的已知条件可得到关于t的方程,解方程即可得知是否存在t的值.
解答 解:
(1)∵在平行四边形ABCD中,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
∴若△BEF为等腰直角三角形,则BE=BF,
∵点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,AB=6cm,BC=12cm,
∴BE=(6-t)cm,BF=2t,
∴6-t=2t,
∴t=2s,
故答案为2s;
(2)由(1)可知若△DFC为等腰直角三角形,则CF=DC,
∵CF=2tcm,DC=6cm,
∴2t=6,
∴t=3s,
故答案为3s;
(3)存在某一时刻,使△EFB∽△FDC,
∵△EFB∽△FDC,
∴BE:CF=BF:DC,
∴$\frac{6-t}{12-2t}=\frac{2t}{6}$,
整理得:2t2-15t+18=0,
即(2t-3)(t-6)=0,
解得:t=1.5或t=6(舍),
∴当t=1.5时,△EFB∽△FDC.
点评 本题综合考查了和相似三角形有关的问题,用到的知识点有矩形的判定和性质、等腰直角三角形的判定和性质、一元二次方程的运用以及相似三角形的判定和性质,特别是(3)小问得到关于t的一元二次方程是解题关键.

练习册系列答案
相关题目
17. 小明从上面观察如图所示的两个物体,看到的是( )
小明从上面观察如图所示的两个物体,看到的是( )
 小明从上面观察如图所示的两个物体,看到的是( )
小明从上面观察如图所示的两个物体,看到的是( )| A. |  | B. |  | C. |  | D. |  |

 已知AB⊥BD,ED⊥BD,EC⊥AC,且AC=CE,AB=6,DE=4,则BD=10.
已知AB⊥BD,ED⊥BD,EC⊥AC,且AC=CE,AB=6,DE=4,则BD=10.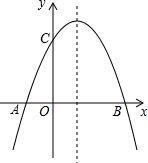 抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点.
抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点. 如图,在平面直角坐标系中,将一块腰长为$\sqrt{5}$的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,顶点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上.
如图,在平面直角坐标系中,将一块腰长为$\sqrt{5}$的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,顶点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上. 如图,△ABC的三条角平分线交于O点,已知△ABC的周长为20,OD⊥AB,OD=5,则△ABC的面积=50.
如图,△ABC的三条角平分线交于O点,已知△ABC的周长为20,OD⊥AB,OD=5,则△ABC的面积=50. 如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )
如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )