题目内容

20．计算：（-1）0+|1-$\sqrt{3}$|=$\sqrt{3}$．

分析 首先利用零指数幂的性质以及绝对值的性质分别化简得出答案．

解答 解：原式=1+$\sqrt{3}$-1
=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 此题主要考查了实数运算，正确化简各数是解题关键．

练习册系列答案
相关题目
10．计算：$\root{3}{0.008}$=0.2．
11．在平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别为（0，3）、（-1，0），将平行四边形ABOC绕点O顺时针旋转90°，得到四边形A′B′OC′，抛物线经过点C、A、A′．

（1）求此抛物线的解析式；
（2）在第一象限的抛物线上有一点P，使得三角形PAA′的面积等于平行四边形ABOC的面积，设点P的横坐标为m（m＞0），求m的值；
（3）若将OB′所在直线沿y轴上下平移得到直线l，当点C′关于直线l的对称点恰好在抛物线上时，直接写出此时直线l的解析式．
8．某漆器厂接到制作240件漆器的订单，为了尽快完成任务，该厂实际每天制作的件数比原来每天多50%，结果提前10天完成任务，原来每天制作多少件？
15．如图是用大小相同的正方形摆放成的一组有规律的图案，图案一需要2个正方形；图案二需要5个正方形；图案三需要10个正方形；图案四需要17个正方形；…按此规律摆下去，图案三十需要正方形个数是（　　）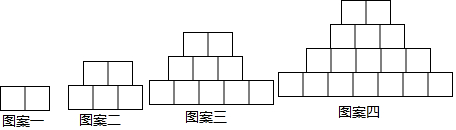
A．902B．901C．900D．899
5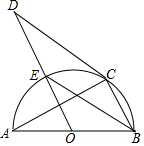．如图，AB是半圆O的直径，C是半圆O上一点，CD是⊙O的切线，OD∥BC，OD与半圆O交于点E，则下列结论中不一定正确的是（　　）
A．AC⊥BCB．BE平分∠ABCC．BE∥CDD．∠D=∠A
12．某市政府大力扶持大学生创业，李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯，销售过程中发现，每月销售量y（件）与销售单价x（元）之间可近似的看作一次函数：y=-10x+500．
（1）李明每月获得利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
（2）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他的销售单价应该定在什么范围合适？他每月的成本最少需要多少元？
9．某大型商场进了一批成本为8元/件的儿童背心，调查发现，这种背心每周的销售量y（件）与它的定价x（元/件）的关系如下表；（x取整数）
x（元/件）10121416
y（件）200180160140
（1）求这种儿童背心每周的销售量y（件）与它的定价x（元/件）之间的函数关系式（不必写出自变量x取值范围）；
（2）为使商场每周获得最大利润，试问这种背心定价应为多少？最大利利润是多少？
（3）若商场每周想要获得不低于1050元的利润，试确定这种儿童背心的定价x（元/件）的取值范围．
10．在平面直角坐标系xOy中，规定：抛物线y=a（x-h）2+k的伴随直线为y=a（x-h）+k．例如：抛物线y=2（x+1）2-3的伴随直线为y=2（x+1）-3，即y=2x-1．
（1）在上面规定下，抛物线y=（x+1）2-4的顶点坐标为（-1，-4），伴随直线为y=x-3，抛物线y=（x+1）2-4与其伴随直线的交点坐标为（0，-3）和（-1，-4）；
（2）如图，顶点在第一象限的抛物线y=m（x-1）2-4m与其伴随直线相交于点A，B（点A在点B的左侧），与x轴交于点C，D．
①若∠CAB=90°，求m的值；
②如果点P（x，y）是直线BC上方抛物线上的一个动点，△PBC的面积记为S，当S取得最大值$\frac{27}{4}$时，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网