题目内容
设x,y是大于零的实数,且
=
,
+
=
,则
+
= .
| sinθ |
| x |
| cosθ |
| y |
| cos2θ |
| x2 |
| sin2θ |
| y2 |
| 14 |
| x2+y2 |
| x |
| y |
| y |
| x |
考点:互余两角三角函数的关系,比例的性质
专题:计算题
分析:根据比例的性质由
=
得
=
,由三角函数的关系有
=tanθ,则tanθ=
,在△ABC中,∠C=90°,AC=x,BC=y,根据锐角三角函数的定义得到
sinθ=
,cosθ=
,则
+
=
可化为
•
+
•
=
,化简后得
+
=14,配方后得到(
+
)2=16,然后两边开方取算术平方根即可.
| sinθ |
| x |
| cosθ |
| y |
| sinθ |
| cosθ |
| x |
| y |
| sinθ |
| cosθ |
| x |
| y |
sinθ=
| x | ||
|
| y | ||
|
| cos2θ |
| x2 |
| sin2θ |
| y2 |
| 14 |
| x2+y2 |
| y2 |
| x2+y2 |
| 1 |
| x2 |
| x2 |
| x2+y2 |
| 1 |
| y 2 |
| 14 |
| x2+y2 |
| y2 |
| x2 |
| x2 |
| y2 |
| y |
| x |
| x |
| y |
解答:解:∵
=
,
∴
=
,而
=tanθ,
∴tanθ=
,
如图,在△ABC中,∠C=90°,AC=x,BC=y,
∴AB=
,
∴sinθ=
,cosθ=
,
而
+
=
,
∴
•
+
•
=
,
∴
+
=14,
∴(
+
)2-2=14,
∴(
+
)2=16,
而x,y是大于零的实数,
∴
+
=4.
故答案为4.
| sinθ |
| x |
| cosθ |
| y |

∴
| sinθ |
| cosθ |
| x |
| y |
| sinθ |
| cosθ |
∴tanθ=
| x |
| y |
如图,在△ABC中,∠C=90°,AC=x,BC=y,
∴AB=
| x2+y2 |
∴sinθ=
| x | ||
|
| y | ||
|
而
| cos2θ |
| x2 |
| sin2θ |
| y2 |
| 14 |
| x2+y2 |
∴
| y2 |
| x2+y2 |
| 1 |
| x2 |
| x2 |
| x2+y2 |
| 1 |
| y 2 |
| 14 |
| x2+y2 |
∴
| y2 |
| x2 |
| x2 |
| y2 |
∴(
| y |
| x |
| x |
| y |
∴(
| y |
| x |
| x |
| y |
而x,y是大于零的实数,
∴
| y |
| x |
| x |
| y |
故答案为4.
点评:本题考查了锐角三角函数的定义:在直角三角形中,一锐角的正弦等于它的对边与斜边的比值;一锐角的余弦等于它的邻边与斜边的比值;一锐角的正切等于它的对边与它的邻边的比值.也考查了勾股定理、完全平方公式以及比例的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列事件是必然事件的是( )
| A、通常加热到100°C时,水沸腾 |
| B、掷一次骰子,向上一面是6点 |
| C、度量三角形的内角和,结果是180° |
| D、某射击运动员射击一次,命中靶心 |
 如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )| A、6 | B、8 | C、12 | D、16 |
下列方程中,无实数根的方程是( )
| A、x2-3x+2=0 | ||
| B、(x-3)2+2=x2 | ||
C、
| ||
D、
|
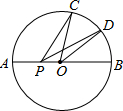 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,
 表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是
表中已经填2、0、1、2四个数,每行中右边数减去左边数都相等,每列中下边数减去上边数也都相等,那么这表中16个数的总和是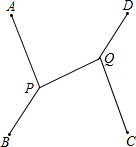 A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?
A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?