题目内容
7.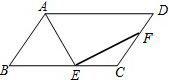 如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.
如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.
分析 注意到AE既是角平分线又是EF的垂线,于是根据三线合一构造出等腰三角形,即双向延长EF分别交AB、AD于M、N,则AM=AN.又由AD∥BC可推出BA=BE,由BC=7,DF=3,EC=CF可求出CE=CF=2,结合tan∠AEB=3,算出AE、ME的长度,从而求出△AMN的面积,接着利用相似三角形的面积之比等于相似比的平方这一性质可分别算出△BME、△CEF、△DFN的面积,再用割补法算出平行四边形ABCD的面积.
解答 解:如图,延长EF交AD于N,延长FE交AB于点M,
∵∠BAE=∠EAD,
∴∠BAE=∠AEB,
∴AB=BE,
设CF=x,
∵CF=EC,DF=3,
∴EC=x,CD=AB=BE=3+x,
∵BC=BE+CE=7,
∴x=2,AB=BE=CD=5,
显然△BEM∽△CEF∽△DNF,
∴BM=BE=5,DN=DF=3,
∴AM=AN=10,
∵AE⊥EF,
∴tan∠AEB=tan∠BAE=3=$\frac{ME}{AE}$,
∴AE=$\sqrt{10}$,ME=3$\sqrt{10}$,
∴S△AMN=$\frac{1}{2}$×MN×AE=30,
∴${S}_{△BME}=\frac{1}{4}{S}_{△AMN}$=$\frac{15}{2}$,
∴${S}_{△CEF}=\frac{4}{25}{S}_{△BME}$=$\frac{6}{5}$,
∴${S}_{△DFN}=\frac{9}{4}{S}_{△CEF}$=$\frac{27}{10}$,
∴SABCD=S△AMN-S△BEM-S△BFN+S△CEF=21.
点评 本题考查了平行四边形的性质、角平分性的性质、相似三角形的判定与性质、解三角形等重要知识点,有一定难度.识别出AE的三线合一性质并正确作出辅助线是解答本题的关键.

| 销售量(万件) | 平均每件产品的利润(元) | |
| 网上销售 | x | 当0<x≤2时,y1=140 |
| 当2≤x<6时,y1=-5x+150 | ||
| 批发部销售 | n | 当0<n≤2时,y2=120 |
| 当2≤n<6时,y2=-5n+130 |
②y2与x的函数关系为:当0<x≤4时,y2=5x+100;当4≤x<6时,y2=120.
(2)求每年该公司销售这种花卉产品的总利润w(万元)与网上销售数量x(万件)的函数关系式,并指出x的取值范围;
(3)该公司每年网上、批发部的销售量各为多少万件时,可使公司每年的总利润最大?最大值为多少万元?
| A. | 80° | B. | 80°或100° | C. | 100° | D. | 160°或20° |
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)本周内每股最高价多少元?最低价是多少元?
| A. | x1=0,x2=5 | B. | x1=0,x2=-5 | C. | x1=0,x2=$\frac{1}{5}$ | D. | x1=0,x2=-$\frac{1}{5}$ |
 如图,已知抛物线y=x2+bx+c与一直线相交于A(-1,0),C(2,-3)两点,与y轴交于点N,其顶点为D.
如图,已知抛物线y=x2+bx+c与一直线相交于A(-1,0),C(2,-3)两点,与y轴交于点N,其顶点为D. 如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3$\sqrt{2}$,BG=4,则GH的长为$\frac{8\sqrt{10}}{11}$.
如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3$\sqrt{2}$,BG=4,则GH的长为$\frac{8\sqrt{10}}{11}$.