题目内容
3．下列命题：①有两个角和一个角的对边对应相等的两个三角形全等；②有一边和一个角对应相等的两个等腰三角形全等；③有一边对应相等的两个等边三角形全等；④一个锐角和一条边对应相等的两个直角三角形全等．其中是真命题的是（ ）| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
分析 根据全等三角形的判定定理（SAS，ASA，AAS，SSS）判断即可．
解答 解：∵有两个角和其中一个角的对边对应相等的两个三角形全等符合AAS定理，∴①正确；
∵全等三角形的判定定理有SAS，ASA，AAS，SSS，∴符合两个条件有一边和一个角对应相等不能推出两三角形全等，∴②错误；
∵根据等边三角形的三边都相等，推出有一边相等的两个等边三角形的三边都相等，即符合SSS定理，∴③正确；
∵一个锐角和一条对应边相等的两个直角三角形符合AAS或ASA定理，∴④正确；
故选B．
点评 本题考查了全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．
练习册系列答案
相关题目
13．若点P（m，n）在第二象限，则点Q（m，-n）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
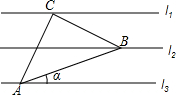已知l1∥l2∥l3，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个项点分别在这三条平行直线上，则sinα的值是$\frac{\sqrt{10}}{10}$．
18．
如图是10个棱长为a的正方体摆放成的图形，则这个图形的表面积为（ ）
如图是10个棱长为a的正方体摆放成的图形，则这个图形的表面积为（ ）| A． | 60a2 | B． | 24a2 | C． | 36a2 | D． | 48a2 |
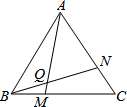如图，已知△ABC中，AB=BC=AC，∠ABC=∠BCA=∠CAB=60°，M、N分别在△ABC的BC、AC边上，且BM=CN，AM、BN交于点Q．求证：∠BQM=60°．
15．已知x2=9，|y|=2，xy＜0，则x+y的值等于（ ）
| A． | 5或-5 | B． | 1或-1 | C． | 5或1 | D． | -5或-1 |
国家食品药品监督管理局对某品牌火腿抽检中，有四包真空小包装火腿，每包以标准克数（450g）为基准，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的是（ ）