Question

7．点C、D为线段AB的垂直平分线上的两点．
（1）如图，当点C、D在线段AB的两侧时，你认为∠CAD与∠CBD相等吗？为什么？
（2）如图，当点C、D在线段AB的同侧时，你认为∠CAD与∠CBD相等吗？为什么？

Answer 1

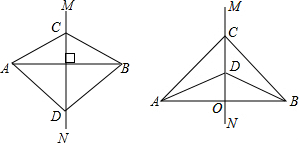
分析 （1）根据线段的垂直平分线的性质得到CA=CB，DA=DB，证明△CAD≌△CBD，得到答案；
（2）根据线段的垂直平分线的性质和等腰三角形的性质证明结论．

解答 解：（1）∠CAD=∠CBD，
证明：∵点C、D为线段AB的垂直平分线上的两点，
∴CA=CB，DA=DB，
在△CAD和△CBD中，
$\left\{\begin{array}{l}{CA=CB}\\{DA=DB}\\{CD=CD}\end{array}\right.$，
∴△CAD≌△CBD，
∴∠CAD=∠CBD；
（2）∵点C为线段AB的垂直平分线上的点，
∴CA=CB，∴∠CAB=∠CBA，
∵点D为线段AB的垂直平分线上的点，
∴DA=DB，∴∠DAB=∠DBA，
∴∠CAD=∠CBD．

点评 此题主要考查线段的垂直平分线的性质等几何知识，线段的垂直平分线上的点到线段的两个端点的距离相等．