题目内容
17.△ABC的三边长分别为3,$\sqrt{3}$,$\sqrt{15}$,△A1B1C1的两边长分别为1和$\sqrt{5}$,当△A1B1C1的第三边长为$\sqrt{3}$时,△ABC与△A1B1C1相似.分析 设△A1B1C1的第三边长为a,分两种情况:①当$\sqrt{5}$为最长边时,由三边成比例得出a=$\sqrt{3}$;②当第三边长为最长边时,$\frac{\sqrt{3}}{1}≠\frac{3}{\sqrt{15}}$,得出△ABC与△A1B1C1不相似;即可得出结果.
解答 解:设△A1B1C1的第三边长为a,分两种情况:
①当$\sqrt{5}$为最长边时,$\frac{3}{a}=\frac{\sqrt{3}}{1}=\frac{\sqrt{15}}{\sqrt{5}}$,
解得:a=$\sqrt{3}$;
②当第三边长为最长边时,$\frac{\sqrt{3}}{1}≠\frac{3}{\sqrt{15}}$,
∴△ABC与△A1B1C1不相似;
综上所述:当第三边长为$\sqrt{3}$时,△ABC与△A1B1C1相似;
故答案为:$\sqrt{3}$.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,由三边成比例得出三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.当x=2时,代数式(x-1)(x2-2x+1)的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.若3x2-3x+2-x2-3x+3=Ax2-Bx+C,则A,B,C的值为( )
| A. | 4,-6,5 | B. | 2,0,-1 | C. | 2,-6,5 | D. | 2,6,5 |
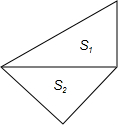 将一副三角尺按如图放置,求上下两块三角尺的面积比S1:S2.
将一副三角尺按如图放置,求上下两块三角尺的面积比S1:S2.