题目内容
11.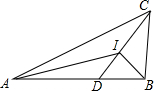 如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )
如图,在△ABC中,AB=6,BC=3,CA=7,I为△ABC的内心,连接CI并延长交AB于点D.记△CAI的面积为m,△DAI的面积为n,则$\frac{m}{n}$=( )| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{4}$ |
分析 由I为△ABC的内心知,AI是△ACD的角平分线,BI是△BCD的角平分线,根据角平分线定理得出$\frac{IC}{ID}$=$\frac{AC}{AD}$=$\frac{BC}{BD}$,利用三角形的面积公式可知同高的两个三角形面积之比等于底边之比,得到$\frac{m}{n}$=$\frac{IC}{ID}$,再由等比定理得出$\frac{m}{n}$=$\frac{IC}{ID}$=$\frac{AC+BC}{AD+BD}$=$\frac{7+3}{6}$=$\frac{5}{3}$.
解答 解:∵I为△ABC的内心,
∴AI是△ACD的角平分线,BI是△BCD的角平分线,
∴$\frac{IC}{ID}$=$\frac{AC}{AD}$=$\frac{BC}{BD}$,
∵$\frac{m}{n}$=$\frac{IC}{ID}$,
∴$\frac{m}{n}$=$\frac{IC}{ID}$=$\frac{AC+BC}{AD+BD}$=$\frac{7+3}{6}$=$\frac{5}{3}$.
故选C.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了角平分线定理,三角形的面积,等比定理.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
17.下列运算正确是( )
| A. | a•a3=a3 | B. | (ab)3=a3b | C. | a8÷a4=a2 | D. | (a3)2=a6 |
1.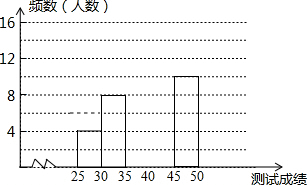 某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
(1)求此次抽查了多少名学生的成绩;
(2)通过计算将频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请估计本次测试九年级学生中成绩优秀的人数.
 某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:| 组别 | 成绩x分 | 人数 | 频率 |
| 1组 | 25≤<30 | 4 | 0.08 |
| 2组 | 30≤x<35 | 8 | 0.16 |
| 3组 | 35≤x<40 | a | 0.32 |
| 4组 | 40≤x<45 | b | c |
| 5组 | 45≤x<50 | 10 | 0.2 |
(2)通过计算将频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请估计本次测试九年级学生中成绩优秀的人数.
 一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度.
一副三角板按如图所示叠放,其中∠ACB=∠DCE=90°,∠A=30°,∠D=45°,且AC∥DE,则∠BCD=45度.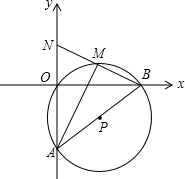 如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
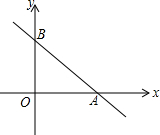 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B,点M在x轴上,要使△ABM是以AB为腰的等腰三角形,那么点M的坐标是($\sqrt{2}$+1,0)、(-$\sqrt{2}$+1,0)或(-1,0).