题目内容
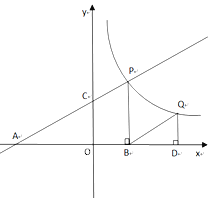
【题目】如图，二次函数
的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数
的图象经过该二次函数图象上点
及点B.
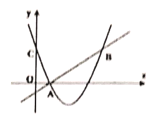
（1）求B点坐标与二次函数的解析式；
（2）根据图象，写出满足
的x的取值范围.
（3）求线段
的长度.
【答案】（1）
；
；（2）
；（3）
【解析】
（1）先将点A代入二次函数解析式中求出m,即可得到二次函数的解析式，进而求出对称轴，再根据对称点的特征求出点B的坐标即可；
（2）根据图像，要求
的x的取值范围，即一次函数图像在抛物线上方所对应的x的范围；
（3）利用A,B的坐标和勾股定理即可求出AB的长度.
（1）将点
代入
中得
解得
∴二次函数的解析式为
对称轴为
当
时，
∵点C和点B关于对称轴对称
（2）
即一次函数图像在抛物线上方
（3）由勾股定理得
【题目】某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、不合格四个等级进行统计，并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
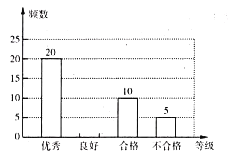
请根据以上信息，解答下列问题：
（1）本次调查随机抽取了______名学生；表中
______，
______；
（2）补全条形统计图；
（3）若全校有2000名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树，经过研究，决定租用当地租车公司一共62辆
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注：载客量指的是每辆客车最多可载该校师生的人数.设学校租用
型号客车
辆，租车总费用为
元.
（1）求与的函数解析式，请直接写出的取值范围；
（2）若要使租车总费用不超过21940元，一共有几种租车方案？哪种租车方案总费用最省？最省的总费用是多少？
