题目内容
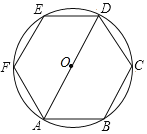
【题目】如图，圆O的半径为1，六边形ABCDEF是圆O的内接正六边形，从A，B，C，D，E，F六点中任意取两点，并连接成线段．
求线段长为2的概率；
求线段长为
的概率．
【答案】（1）
（2）
【解析】
（1）连接AE，过点F作FN⊥AE于点N，得出△AOB是等边三角形，得出OA=AB=BC=CD=DE=EF=AE=1，∠FAE=30°，由直角三角形的性质得出AN=
，AE=
，同理：AC=，画树状图，共有30个等可能的结果，线段长为2的结果有6个，由概率公式即可得出结果；
（2）由树状图可知，共有30个等可能的结果，线段长为的结果有12个，由概率公式即可得出结果．
解：
连接AE，过点F作
于点N，如图1所示：
圆O的半径为1，六边形ABCDEF是圆O的内接正六边形，
，
，
，
，
是等边三角形，
，
，
，
同理：
，
画树状图如图2所示：
共有30个等可能的结果，线段长为2的结果有6个，
线段长为2的概率为
；
由树状图可知，共有30个等可能的结果，线段长为的结果有12个，
线段长为的概率为
．
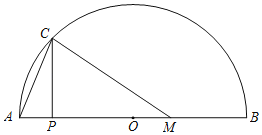
【题目】如图，在半圆弧AB中，直径AB＝6cm，点M是AB上一点，MB＝2cm，P为AB上一动点，PC⊥AB交AB于点C，连接AC和CM，设A、P两点间的距离为xcm，A、C两点间的距离为y1cm，C、M两点间的距离为y2cm．
小东根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究：
下面是小东的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.45 | 3.46 | 4.90 | 5.48 | 6 | |
y2/cm | 4 | 3.74 | 3.46 | 3.16 | 2.83 | 2.45 | 2 |
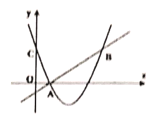
（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；
（3）结合函数图象，解决问题：
①当AC＞CM时，线段AP的取值范围是 ；
②当△AMC是等腰三角形时，线段AP的长约为 ．
