Question

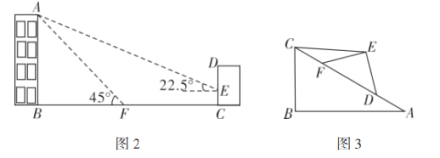
【题目】为了测量竖直旗杆AB的高度，某综合实践小组在地面D处竖直放置标杆CD，并在地面上水平放置一个平面镜E，使得B，E，D在同一水平线上（如图所示）．该小组在F处测得旗杆顶A的仰角为45°，平面镜E的俯角为67°，测得米，在标杆的F处通过平面镜E恰好观测到旗杆顶A（此时）．

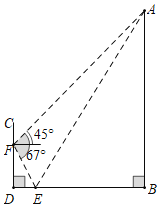
求：（1）平面镜E到标杆底部D的距离．

（2）旗杆AB的高度．

（结果保留整数，参考数据：，，）

Answer 1

【答案】（1）1米；（2）6米

【解析】

（1）作FG⊥AB于G，在Rt△EDF中，根据∠FED的正切函数求解即可；

（2）设AB为x米，根据正切的定义求出FG、BE，根据图形列方程计算，得到答案．

解：（1）作FG⊥AB于G，

∵FG∥BD，

∴∠FED=∠GFE=67°，

在Rt△EDF中，tan∠FED= ，

∴米，

（2）设AB为x米，由题意得，四边形FDBG为矩形，

在Rt△AFG中，∠AFG=45°，

∴FG=AG=x-2.4，

在Rt△AEB中，tan∠AEB= ，

即，

由题意得，，

解得，x≈6，

答：旗杆AB的高度约为6米．