Question

15．如图，直线OC、BC的函数关系式分别为y=x和y=-2x+6，动点P（x，0）在OB上移动（0＜x＜3），过点P作直线l与x轴垂直．
（1）求点C的坐标；
（2）若点A（0，1），当x为何值时，AP+CP最小．
（3）设△OBC中位于直线l左侧部分的面积为s，写出s与x之间的函数关系式；
（4）当x为何值时，直线l平分△OBC的面积？

Answer 1

分析 （1）联立两直线解析式，解方程组即可求得C点坐标；
（2）可求得点A关于x轴的对称点A′坐标，连接A′C交x轴于一点，则该点即为满足条件的点P，利用待定系数法可求得直线A′C的解析式，则可求得P点坐标；
（3）过C作CD⊥x轴于点D，当点P在线段OD上时，设直线l交OC于点E，可用x表示出E点坐标，直接用s=$\frac{1}{2}$OP•PE，可求得s与x的函数关系式，当点P在线段BD上时，设直线l交BC于点F，则可用s=S_△OBC-S_△BPF可求得函数关系式；
（4）利用（3）的结论，可知当点P在线段OD上时才有直线l平分△OBC的面积，则有s=$\frac{1}{2}$S_△OBC，可求得x的值．

解答 解：
（1）联立两直线解析式可得$\left\{\begin{array}{l}{y=x}\\{y=-2x+6}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，
∴C点坐标为（2，2）；
（2）设点A关于x轴的对称点为A′，
∵A（0，1），
∴A′（0，-1），
如图1，连接A′C交x轴于点P，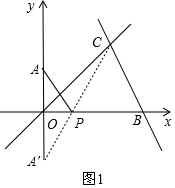

此时PA=PA′，且A′、P、C三点在一条线上，
∴此时PA+PC最小，
设直线A′C解析式为y=kx+b，
∴$\left\{\begin{array}{l}{2k+b=2}\\{b=-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=1.5}\\{b=-1}\end{array}\right.$，
∴直线A′C解析式为y=1.5x-1，
令y=0可得：1.5x-1=0，解得x=$\frac{2}{3}$，
∴当x=$\frac{2}{3}$时，AP+CP最小；
（3）过C作CD⊥x轴，交x轴于点D，
则OD=CD=2，
当点P在线段OD上时，设直线l交OC于点E，如图2，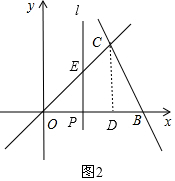

∵P（x，0），
∴E（x，x），
∴OP=PE=x，
∴s=S_△OPE=$\frac{1}{2}$OP•PE=$\frac{1}{2}$x²；
当点P在线段BD上时，设直线l交BC于点F，如图3，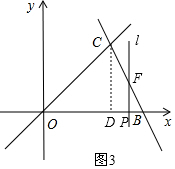

在y=-2x+6中，令y=0可求得x=3，
∴OB=3，
∵P（x，0），
∴F（x，-2x+6），
∴PF=-2x+6，PB=OB-OP=3-x，
∴s=S_△OBC-S_△BPF=$\frac{1}{2}$×3×2-$\frac{1}{2}$（3-x）（-2x+6）=-x²+6x-6，
综上可知s=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}（0≤x≤2）}\\{-{x}^{2}+6x-6（2＜x≤3）}\end{array}\right.$；
（4）由题意可知当直线l平分△OBC的面积时，则点P在线段OD上，即0≤x≤2，
由（3）可知，此时s=$\frac{1}{2}$x²，
∴$\frac{1}{2}$x²=$\frac{1}{2}$S_△OBC，即$\frac{1}{2}$x²=$\frac{1}{2}$×$\frac{1}{2}$×3×2，解x=$\sqrt{3}$或x=-$\sqrt{3}$（舍去），
∴当x=$\sqrt{3}$时，直线l平分△OBC的面积．

点评 本题为一次函数的综合应用，涉及函数图象的交点、轴对称的应用、待定系数法、三角形的面积及分类讨论思想等知识点．在（1）中注意求函数图象交点的方法，在（2）中确定出P点的位置是解题的关键，在（3）中注意分两种情况，在（4）中P点所在的位置．本题考查知识点较多，综合性较强，难度适中．