Question

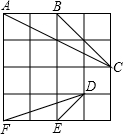在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．
（1）填空：∠DEF=

135

°，DE=

2

；
（2）判断△ABC与△DEF是否相似，并证明你的结论．

Answer 1

分析：（1）由图形可以直接得到：∠FEM和∠DEM的度数，求其和即可；DE的长利用勾股定理即可算出；
（2）根据勾股定理分别计算出△ABC和△DEF的长，再根据三组对应边的比相等的两个三角形相似即可得到结论．

解答：解：（1）根据图形可得：∠FEM=90°，∠DEM=45°，
∴∠DEF=90°+45°=135°，
DE=

12+12

=

2

；

（2）相似，理由如下：
在△ABC中：AB=2，BC=

22+22

=2

2

，AC=

42+22

=2

5

，
在△DEF中：EF=2，DE=

2

，DF=

12+32

=

10

，
∵

AB

DE

=

2

2

=

2

，

BC

EF

=

2 2

2

=

2

，

AC

DF

=

2 5

10

=

2

，
∴

AB

DE

=

BC

EF

=

AC

DF

，
∴△ABC∽△DEF．

点评：此题主要考查了勾股定理，相似三角形的判定，关键是熟练运用勾股定理计算出三角形的三边长．