题目内容
 在5×5的正方形方格中,每个小正方形的边长为1,每个小正方形的顶点称为格点.
在5×5的正方形方格中,每个小正方形的边长为1,每个小正方形的顶点称为格点.(1)在网格中,画出从点A出发的一条线段AB,使端点B落在格点上,且AB=2
| 2 |
(2)在网格中,画出以AB为底边,且腰长为无理数的两个等腰△ABC、△ABC′;
(3)将四边形ACBC′进行适当裁剪,拼成一个正方形.试在(2)中画出的图形中画出裁剪线与拼成的图形.
分析:(1)根据每个小正方形的边长为1,利用勾股定理可得出AB的位置;
(2)根据等腰三角形的性质,得出C点位置是线段AB垂直平分线与格点交点得出即可;
(3)根据正方形的性质结合图形面积得出答案即可.
(2)根据等腰三角形的性质,得出C点位置是线段AB垂直平分线与格点交点得出即可;
(3)根据正方形的性质结合图形面积得出答案即可.
解答: 解:(1)如图所示:AB即为所求;
解:(1)如图所示:AB即为所求;
(2)如图所示,△ABC、△ABC′为所求;
(3)如图所示,正方形即为所求.
 解:(1)如图所示:AB即为所求;
解:(1)如图所示:AB即为所求;(2)如图所示,△ABC、△ABC′为所求;
(3)如图所示,正方形即为所求.
点评:此题主要考查了图形的剪拼以及等腰三角形的性质和正方形的性质以及勾股定理的应用,正确根据勾股定理得出线段长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上. 如图,在4×4的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上、请你在图中画出一个与△ABC相似的△DEF,使得△DEF的顶点都在边长为1的小正方形的顶点上,且△ABC与△DEF的相似比为1:2.
如图,在4×4的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上、请你在图中画出一个与△ABC相似的△DEF,使得△DEF的顶点都在边长为1的小正方形的顶点上,且△ABC与△DEF的相似比为1:2.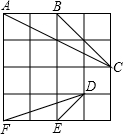 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.