题目内容
已知抛物线的顶点A（1，4）且经过点B（2，3），求此抛物线与x轴的交点坐标．
考点：抛物线与x轴的交点
专题：计算题
分析：根据抛物线顶点坐标设出顶点式，将B坐标代入求出a的值，确定出抛物线解析式，令y=0求出x的值，即可确定出抛物线与x轴的交点坐标．
解答：解：根据题意设抛物线顶点形式为y=a（x-1）2+4，
将B（2，3）代入得：3=a+4，即a=-1，
∴抛物线解析式为y=-x2+2x+3，
令y=0，得到-x2+2x+3=0，即-（x-3）（x+1）=0，
解得：x=3或x=-1，
则抛物线与x轴交点坐标为（-1，0）和（3，0）．
将B（2，3）代入得：3=a+4，即a=-1，
∴抛物线解析式为y=-x2+2x+3，
令y=0，得到-x2+2x+3=0，即-（x-3）（x+1）=0，
解得：x=3或x=-1，
则抛物线与x轴交点坐标为（-1，0）和（3，0）．
点评：此题考查了抛物线与x轴的交点，熟练掌握待定系数法是解本题的关键．
练习册系列答案
相关题目
用长8米的铝材制成一个矩形窗框，使它的面积为5平方米．若设它的一边长为x米，根据题意列出关于x的方程为（ ）
| A、x（8-x）=5 |
| B、x（4+x）=5 |
| C、x（4-x）=5 |
| D、x（8-2x）=5 |
小明同学在“百度”搜索引擎中输入“中国梦”，搜索到相关的结果约为8950000个，这个数用科学记数法表示为（ ）
| A、8.95×107 |
| B、89.5×106 |
| C、8.95×106 |
| D、0.895×107 |
如图，点D、E分别在△ABC的边BA、CA的延长线上，DE∥BC，EC=5，EA=2，△ADE的面积为8，则△ABC的面积为（ ）| A、50 | B、20 | C、18 | D、10 |
如图，已知函数y=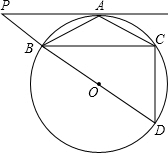
已知：如图⊙O是△ABC的外接圆，P为圆外一点，PA∥BC，且A为劣弧
为了倡导“节约用水，从我做起”的活动，某市政府决定对市直机关500户家庭的用水情况作一次调查，调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果制成了如图所示的条形统计图．