题目内容
13.已知在△ABC中,AB=5,BC=2,且AC为奇数.(1)求△ABC的周长;
(2)判断△ABC的形状.
分析 (1)首先根据三角形的三边关系定理可得5-2<AC<5+2,再根据AC为奇数确定AC的值,进而可得周长;
(2)根据等腰三角形的判定可得△ABC是等腰三角形.
解答 解:(1)由题意得:5-2<AC<5+2,
即:3<AC<7,
∵AC为奇数,
∴AC=5,
∴△ABC的周长为5+5+2=12;
(2)∵AB=AC,
∴△ABC是等腰三角形.
点评 此题主要考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.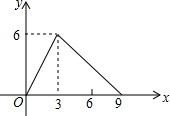 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
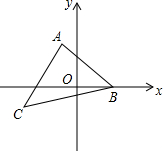 如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)
如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1)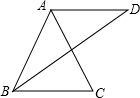 如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.
如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.