题目内容
19.解不等式或不等式组(1)解不等式$\frac{x+3}{5}$≤$\frac{2x-5}{3}$-1,并在数轴上表示解集.
(2)解不等式组$\left\{\begin{array}{l}{\frac{1}{2}(x+4)<2}\\{\frac{x+2}{2}>\frac{x+3}{3}}\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1,最后在数轴上表示出不等式的解集即可.
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)去分母,得3(x+3)<5(2x-5)-15,
整理,得-7x≤-49
∴x≥7.
(2)$\left\{\begin{array}{l}{\frac{1}{2}(x+4)<2①}\\{\frac{x+2}{2}>\frac{x+3}{3}②}\end{array}\right.$
解不等式①,得x<0;
解不等式②,得x>0;
∴不等式组无解.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
10.一组数据x1,x2,x3,…,xn的平均数是a,方差是b,那么数据2x1,2x2,2x3…2xn的平均数和方差分别是( )
| A. | 2a和2b | B. | 2a和4b | C. | 4a和2b | D. | 4a和4b |
4.下列调查中,适宜采用普查的是( )
| A. | 了解重庆市空气质量情况 | B. | 了解长江水流的污染情况 | ||
| C. | 了解重庆市居民的环保意识 | D. | 了解全班同学每周体育锻炼的时间 |
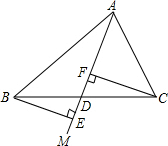 如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).
如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).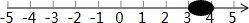 把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.
把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.