题目内容
15.在△ABC中,∠C=90°,a、b、c分别是∠A,∠B,∠C的对边,根据已知条件解直角三角形:(1)c=8$\sqrt{3}$,∠A=60°
(2)a=3$\sqrt{6}$,∠A=30°
(3)a=6,b=2$\sqrt{3}$.
分析 (1)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到b的值,然后利用正切的定义求出a;
(2)先利用互余计算出∠B,再利用含30度对的边等于斜边的一半得到c的值,然后利用正切的定义求出b;
(3)先利用勾股定理计算出c,再利用正切的定义求出∠A,然后利用互余计算∠B.
解答 解:(1)∵∠A=60°,
∴∠B=90°-∠A=90°-60°=30°,
∴b=$\frac{1}{2}$c=$\frac{1}{2}$×8$\sqrt{3}$=4$\sqrt{3}$,
∵tanA=$\frac{a}{b}$,
∴a=4$\sqrt{3}$•tan60°=12;
(2)∵∠A=30°,
∴∠B=60°,c=2a=6$\sqrt{6}$,
∵tanA=$\frac{a}{b}$=$\frac{\sqrt{3}}{3}$,
∴b=9$\sqrt{2}$;
(3)c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$,
∵tanA=$\frac{a}{b}$=$\sqrt{3}$,
∴∠A=60°,
∴∠B=90°-∠A=30°.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
3.股民小胡发现股市行情非常的好,于是在国信证券开户并投入1万元人民币,在周五全部买入了当日收盘价7元一股的“万向前潮”(按规定:股数必须是100股的倍数,且双休日股市停开),因各种原因,股票价格实际每天各有涨跌(涨为正,跌为负),下表是买入后下一周的股价变化情况(单位:元)
(1)请问该股到周五收盘时,每股是多少元?
(2)根据规定,股票每买一次或卖一次都必须缴纳交易税和印花税共计交易总额的$\frac{5}{10000}$,假如小胡以表中周五收盘的价格抛出所以股票,请问这时小胡的账户总金额是多少元元?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| +0.15 | -0.24 | -0.03 | 0 | +0.68 |
(2)根据规定,股票每买一次或卖一次都必须缴纳交易税和印花税共计交易总额的$\frac{5}{10000}$,假如小胡以表中周五收盘的价格抛出所以股票,请问这时小胡的账户总金额是多少元元?
4.下列式子中,是最简二次根式的有( )
①$\sqrt{{a}^{3}}$,②$\sqrt{m-2}$,③$\sqrt{\frac{x}{3}}$,④$\sqrt{8ab}$,⑤$\sqrt{{x}^{2}-{y}^{2}}$.
①$\sqrt{{a}^{3}}$,②$\sqrt{m-2}$,③$\sqrt{\frac{x}{3}}$,④$\sqrt{8ab}$,⑤$\sqrt{{x}^{2}-{y}^{2}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列图形中,轴对称图形的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
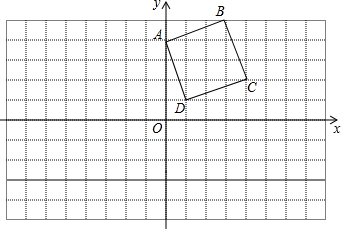 正方形ABCD在直角坐标系中的位置如图所示:
正方形ABCD在直角坐标系中的位置如图所示: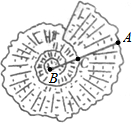 如图是一种贝壳的俯视图,点C为线段AB的黄金分割(AC>BC),已知AB=10cm,则AC长为5$\sqrt{5}$-5cm.(结果保留根号)
如图是一种贝壳的俯视图,点C为线段AB的黄金分割(AC>BC),已知AB=10cm,则AC长为5$\sqrt{5}$-5cm.(结果保留根号)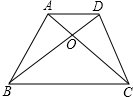 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积.
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积.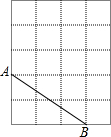 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.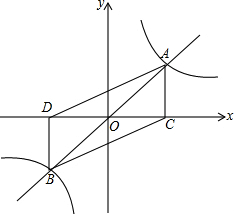 如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.
如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.