题目内容
5.若a、b为有理数,则$\frac{|a|}{a}+\frac{|b|}{b}$=2,-2,0.分析 根据已知分别利用a,b可能的值分析求出即可.
解答 解:∵若a>0,$\frac{|a|}{a}$=$\frac{a}{a}$=1;若a<0,$\frac{|a|}{a}$=$\frac{-a}{a}$=-1,
∴当a>0,b>0,
原式=1+1=2;
当a>0,b<0,
原式=1-1=0;
当a<0,b>0,
原式=-1+1=0;
当a<0,b<0,
原式=-1-1=-2,
综上所述:$\frac{|a|}{a}+\frac{|b|}{b}$的所有可能值为:2,-2,0.
故答案为:2,-2,0.
点评 此题主要考查了有理数的除法以及绝对值,正确分类讨论得出是解题关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
17.若分式$\frac{5a-b}{3a+2b}$有意义,则a,b满足的关是( )
| A. | 3a≠2b | B. | a≠$\frac{1}{5}$b | C. | b$≠-\frac{2}{3}$a | D. | a$≠-\frac{2}{3}$b |
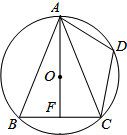 如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.
如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.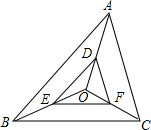 如图,已知O是△ABC内一点,D、E、F分别是OA、OB、OC的中点.求证:△ABC∽△DEF.
如图,已知O是△ABC内一点,D、E、F分别是OA、OB、OC的中点.求证:△ABC∽△DEF.