题目内容
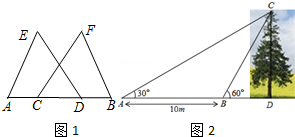
4.某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6米、8米,现在将其扩建成等腰三角形,且扩充部分是以8米为直角边的直角三角形,求扩建后的等腰三角形花圃的面积.分析 利用等腰三角形的性质分别画出符合题意的图形求出即可.
解答  解:如图①所示:S△ABD=$\frac{1}{2}$×8×12=48(m2);
解:如图①所示:S△ABD=$\frac{1}{2}$×8×12=48(m2);
如图②所示:S△ABD=$\frac{1}{2}$×8×10=40(m2);
如图③所示:在Rt△ACD中,AC2+DC2=AD2,
即82+x2=(x+6)2,
解得:x=$\frac{7}{3}$,
故S△ABD=$\frac{1}{2}$×8×(6+$\frac{7}{3}$)=$\frac{100}{3}$(m2).
点评 此题主要考查了应用设计与作图,正确利用等腰三角形的性质求出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.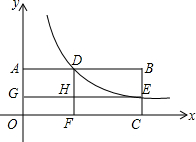 如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
 如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=$\frac{k}{x}$与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{5}{2}$ | D. | 2$\sqrt{2}$ |
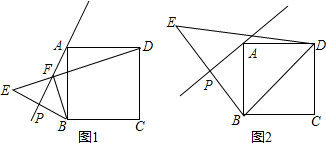
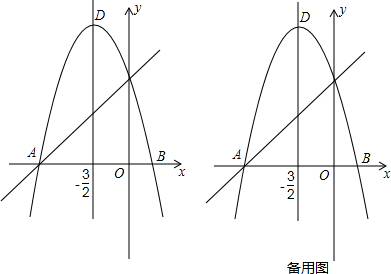
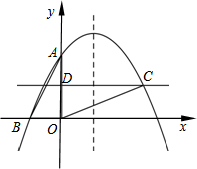 如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.
如图,在平面直角坐标系中,一条抛物线经过点A(0,2)、B(-1,0),且对称轴为直线x=1.点C是抛物线上x轴上方任意一点,直线CD平行于x轴,与y轴交于点D.设点C的横坐标为x.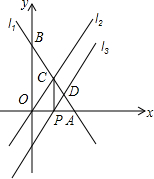 如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.
如图,已知直线l1:y=-2x+8与两坐标轴分别相交于A、B两点,与直线l2:y=2x相交于点C,点P为x轴上的一个动点,过点P的直线,l3∥l2,且与l1相交于点D.