题目内容
下列各组数中，能构成直角三角形的是（ ）
| A、4，5，6 | ||
B、1，1，
| ||
| C、6，8，11 | ||
| D、4，11，13 |
考点：勾股定理的逆定理
专题：
分析：知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形；否则不是．
解答：解：A、42+52≠62，不能构成直角三角形，故错误；
B、12+12=（
）2，能构成直角三角形，故正确；
C、82+62≠112，能构成直角三角形，故错误；
D、42+112≠132，不能构成直角三角形，故错误．
故选：B．
B、12+12=（
| 2 |
C、82+62≠112，能构成直角三角形，故错误；
D、42+112≠132，不能构成直角三角形，故错误．
故选：B．
点评：本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
综合自测系列答案
相关题目
若
=3-a，则a与3的大小关系是（ ）
| (a-3)2 |
| A、a＜3 | B、a＞3 |
| C、a≤3 | D、a |
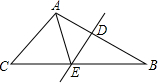如图，E是△ABC的BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=1.5，则△ABC的周长是（ ）| A、8.5 | B、10 |
| C、11.5 | D、13 |
已知2a+3b=5，2a-3b=3，那么（4a2-9b2）2的值是（ ）
| A、15 | B、30 | C、225 | D、22 |
下列计算正确的是（ ）
| A、|-2|=2 | ||
| B、-2-1=2 | ||
| C、20=0 | ||
D、
|
已知点P1（3a-1，5）和P2（2，3b+1）关于x轴对称，则（a+b）2011的值为（ ）
| A、0 |
| B、-1 |
| C、1 |
| D、（-3）2011 |
图1是一个边长为1的等边三角形和一个边长为
的菱形的组合图形，其周长为4；以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第2014个图形的周长是（ ）
| 1 |
| 2 |
| A、22014 |
| B、24028 |
| C、22015 |
| D、22017 |