题目内容
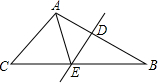如图，E是△ABC的BC上的一点，DE垂直平分AB，△ACE的周长是8.5，AB=1.5，则△ABC的周长是（ ）| A、8.5 | B、10 |
| C、11.5 | D、13 |
考点：线段垂直平分线的性质
专题：
分析：DE垂直平分AB，可得AE=EB，△ABC的周长可以化为△ACE的周长加上AB，根据已知条件可进行求解．
解答：解：∵DE垂直平分AB，
∴AE=EB．
又∵△ACE的周长是8.5，即AC+CE+AE=8.5，
∴△ABC的周长=AC+CE+EB+AB=AC+CE+AE+AB=8.5+1.5=10．
故选B．
∴AE=EB．
又∵△ACE的周长是8.5，即AC+CE+AE=8.5，
∴△ABC的周长=AC+CE+EB+AB=AC+CE+AE+AB=8.5+1.5=10．
故选B．
点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
一次函数y=-kx+b的图象（其中k＜0，b＞0）大致是（ ）
A、 |
B、 |
C、 |
D、 |
已知半径分别4和7的两圆外离，则它们的圆心距可能是（ ）
| A、6 | B、3或11 | C、2 | D、22 |
若关于x的不等式组
有实数解，则实数m的取值范围是（ ）
|
| A、m≤2 | B、m＜2 |
| C、m＞2 | D、m≥2 |
下列各组数中，能构成直角三角形的是（ ）
| A、4，5，6 | ||
B、1，1，
| ||
| C、6，8，11 | ||
| D、4，11，13 |
方程x2-9=0的根为（ ）
| A、3 | B、-3 | C、±3 | D、无实数根 |
