题目内容
16.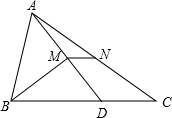 如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN=$\frac{3}{2}$.
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN=$\frac{3}{2}$.
分析 根据题目的已知条件易求DC的长为3,易证MN是三角形ADC的中位线,由三角形中位线定理即可求出MN 的长.
解答 解:∵BD=AB,BM⊥AD于点M,
∴AM=DM,
∵N是AC的中点,
∴AN=CN,
∴MN是三角形ADC的中位线,
∴MN=$\frac{1}{2}$DC,
∵AB=5,BC=8,
∴DC=3,
∴MN=$\frac{3}{2}$,
故答案是:$\frac{3}{2}$.
点评 此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y是x的一次函数,下表列出两套符合条件的课桌椅的高度.
(1)请确定课桌高度与椅子高度的函数关系式;
(2)现有一张高80cm的课桌和一张高为43cm的椅子,它们是否配套?为什么?
| 第一套 | 第二套 | |
| 椅子高度x(cm) | 42 | 38 |
| 课桌高度y(cm) | 74 | 70 |
(2)现有一张高80cm的课桌和一张高为43cm的椅子,它们是否配套?为什么?
11.已知一次函数y=kx+b的图象一定不通过第二象限,则系数k,b一定满足( )
| A. | k>0,b>0 | B. | k>0,b≤0 | C. | k<0,b>0 | D. | k<0,b<0 |
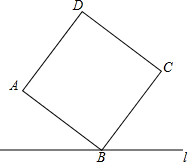 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.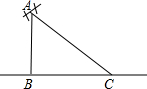 如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )