题目内容
2.观察下列各式:$\frac{2}{1}$×2=$\frac{2}{1}$+2,$\frac{3}{2}$×3=$\frac{3}{2}$+3,$\frac{4}{3}$×4=$\frac{4}{3}$+4,$\frac{5}{4}$×5=$\frac{5}{4}$+5,$\frac{6}{5}$×6=$\frac{6}{5}$+6,…通过观察,你发现了什么规律?设n为正整数,用关于n的等式表示这个规律.
分析 通过观察可以看出两个数的和等于两个数的积,分数的分母比分子小一,而相乘的整数和相加的整数也比分母大一,由此规律得出答案即可.
解答 解:由所给的各式可知,设n为正整数,则分子为n+1,另一个因数和加数也为n+1,因此可知规律为:
$\frac{(n+1)}{n}$×(n+1)=$\frac{(n+1)}{n}$+(n+1).
点评 此题考查数字的变化规律,找出式子之间的联系,由特殊找出一般规律解决问题.

练习册系列答案
相关题目
12.下表是2015年6月份的月历表,任意圈出一横行或一竖列相邻的三个数,则这三个数的和不可能是( )
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
| A. | 24 | B. | 43 | C. | 57 | D. | 69 |
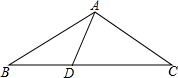 如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.
如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.
 有这样一个小游戏,如图1-4号四个气球上分别贴有四个结论:①已知a=-5,|a|=|b|,则b的值等于-5;②如果m=-2015,那么-m的值是2015;③一个数的绝对值越大,这个数就越大;④$\frac{1}{5}$的相反数是-0.2,将贴有正确结论的气球全部打爆者获胜,你认为应该打爆的气球是②④(写出气球的号数).
有这样一个小游戏,如图1-4号四个气球上分别贴有四个结论:①已知a=-5,|a|=|b|,则b的值等于-5;②如果m=-2015,那么-m的值是2015;③一个数的绝对值越大,这个数就越大;④$\frac{1}{5}$的相反数是-0.2,将贴有正确结论的气球全部打爆者获胜,你认为应该打爆的气球是②④(写出气球的号数).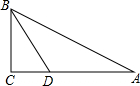 如图.已知△ABC中,∠C=90°,∠A=30°,BD平分∠CBA,且交AC于点D,AC=1.求AD的长.
如图.已知△ABC中,∠C=90°,∠A=30°,BD平分∠CBA,且交AC于点D,AC=1.求AD的长.