题目内容
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:BE=BF;
(2)若∠CAE=30°,求∠ACF度数.
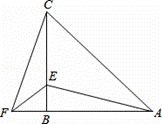
20、
(1)证明:在Rt△ABE和Rt△ADF中
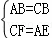 ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=BF; ------------------ 4分
(2)解:∵AB=CB,∠ABC=90°,
∴∠BAC=∠BCA=45°,
∵∠CAE=30°,
∴∠BAE=45°﹣30°=15°,
∵Rt△ABE≌Rt△ADF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠BCA=15°+45°=60°.

练习册系列答案
相关题目
在平面直角坐标系中,⊙A,⊙B的圆心坐标分别是A(3,0),B(0,4),若这两圆的半径分别是3,4,则这两圆的位置关系是( )
|
| A. | 内含 | B. | 相交 | C. | 外切 | D. | 外离 |
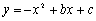 的图象经过
的图象经过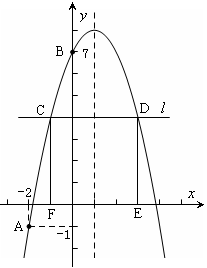 A(-2,-1),B(0,7)两点.
A(-2,-1),B(0,7)两点.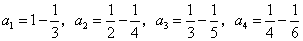 ,….试猜想,第
,….试猜想,第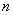 个等式(
个等式(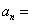
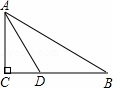
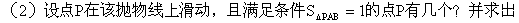

 某公司计划在一座圆锥形土丘上铺满草皮,土丘高50米坡度 ,则草皮面积为_______(结果可含根号, )
某公司计划在一座圆锥形土丘上铺满草皮,土丘高50米坡度 ,则草皮面积为_______(结果可含根号, )