题目内容
12．
如图，已知⊙O的直径CD垂直于弦AB，∠ACD=22.5°，若CD=6cm，求AB的长．
分析 连接OA、OB，根据圆周角定理求出∠AOD=45°，根据垂径定理求出∠AOB=90°，根据勾股定理计算即可．
解答 解：连接OA、OB，
∵∠ACD=22.5°，
∴∠AOD=45°，
∵直径CD垂直于弦AB，
∴$\widehat{AD}$=$\widehat{BD}$，
∴∠AOB=90°，
又∵OA=3，
∴AB=3$\sqrt{2}$cm．
点评 本题考查的是垂径定理和勾股定理的应用，正确作出辅助线、构造直角三角形、灵活运用定理是解题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2．若$\sqrt{{{（1-m）}^2}}$=m-1，则m的取值范围是（ ）
| A． | m≥1 | B． | m≤1 | C． | m=1 | D． | 一切实数 |
3．某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天的生产量与计划生产量相比有出入，下表是某周的生产情况（超产记为正，少产记为负）：
（1）根据记录的数据可知该厂星期四生产自行车210辆．
（2）产量最多的一天比产量最少的一天多生产自行车28辆．
（3）根据记录的数据可知该厂本周实际生产自行车多少辆？
（4）该厂实际每周计件工资制，每生产一辆自行车可得50元，若超额完成任务，则超过部分每辆另奖20元，若未完成任务，则每少生产一辆扣25元，那么该厂工人这一周的工资总额是多少元？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减 | +6 | -3 | -2 | +10 | -8 | +18 | -10 |
（2）产量最多的一天比产量最少的一天多生产自行车28辆．
（3）根据记录的数据可知该厂本周实际生产自行车多少辆？
（4）该厂实际每周计件工资制，每生产一辆自行车可得50元，若超额完成任务，则超过部分每辆另奖20元，若未完成任务，则每少生产一辆扣25元，那么该厂工人这一周的工资总额是多少元？
解下列不等式，并把解集在数轴上表示出来．
4．
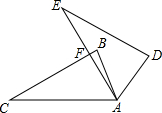如图，△ABC中，∠C=30°，将△ABC绕点A顺时针旋转60°得△ADE，AE与BC交于F，则∠AFB为多少度？（ ）
如图，△ABC中，∠C=30°，将△ABC绕点A顺时针旋转60°得△ADE，AE与BC交于F，则∠AFB为多少度？（ ）| A． | 70° | B． | 90° | C． | 60° | D． | 55° |
如图，将直角三角形绕直角边AB旋转一周，所得的几何体从正面看到的图形是（ ）
2．已知点M（2，1）和点N（1，-2）在直线l：y=kx+b上，则直线l与x轴的交点坐标是（ ）
| A． | （0，-5） | B． | （-5，0） | C． | （0，$\frac{5}{3}$） | D． | （$\frac{5}{3}$，0） |