题目内容
12.先化简,再求代数式$(\frac{1}{x+y}-\frac{1}{{{x^2}+xy}})÷\frac{x-1}{x}$的值,其中$x=\sqrt{2}-2cos{60°}$,y=tan45°.分析 先根据分式混合运算的法则把原式进行化简,再求出x、y的值代入进行计算即可.
解答 解:原式=[$\frac{1}{x+y}$-$\frac{1}{x(x+y)}$]•$\frac{x}{x-1}$
=$\frac{x-1}{x(x+y)}$•$\frac{x}{x-1}$
=$\frac{1}{x+y}$.
当x=$\sqrt{2}$-2cos60°=$\sqrt{2}$-2×$\frac{1}{2}$=$\sqrt{2}$-1,y=tan45°=1时,
原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
3.64的算术平方根是( )
| A. | 4 | B. | ±4 | C. | 8 | D. | ±8 |
20.下列计算正确的是( )
| A. | a+2a2=3a3 | B. | (a3)2=a5 | C. | a3•a2=a6 | D. | a6÷a2=a4 |
17.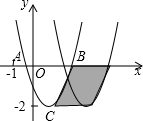 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
正确的是( )
 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
正确的是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
19.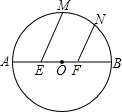 如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )
如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )
 如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )
如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为$\widehat{AB}$上两点,且∠MEB=∠NFB=60°,则EM+FN=( )| A. | $\frac{\sqrt{33}}{2}$ | B. | $\sqrt{33}$ | C. | 2$\sqrt{33}$ | D. | 33 |