题目内容
请你猜想:
-
与
-
(n是大于1的整数)的大小关系,并加以证明.
| n+1 |
| n |
| n |
| n-1 |
考点:二次根式的混合运算,实数大小比较
专题:计算题
分析:利用倒数法比较大小:先利用分母有理化得到
=
+
,
=
+
,然后比较倒数的方法比较原来两数的大小.
| 1 | ||||
|
| n+1 |
| n |
| 1 | ||||
|
| n |
| n-1 |
解答:解:
-
<
-
.理由如下:
∵
=
+
,
=
+
,
而
>
,
∴
>
,
而
-
>0,
-
>0,
∴
-
<
-
.
| n+1 |
| n |
| n |
| n-1 |
∵
| 1 | ||||
|
| n+1 |
| n |
| 1 | ||||
|
| n |
| n-1 |
而
| n+1 |
| n-1 |
∴
| 1 | ||||
|
| 1 | ||||
|
而
| n+1 |
| n |
| n |
| n-1 |
∴
| n+1 |
| n |
| n |
| n-1 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
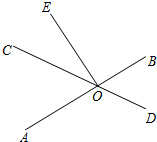 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=30°,求∠AOD的度数. 如图,四边形ABCD,在四边形内找一点O,使得线段AO、BO、CO、DO的和最小.(画出即可,不写作法)
如图,四边形ABCD,在四边形内找一点O,使得线段AO、BO、CO、DO的和最小.(画出即可,不写作法)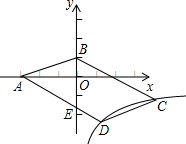 如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=