题目内容
18．当a＞0，b＜0，c＞0时，抛物线y=ax2+bx+c的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由a＞0可以得到开口方向向上，由b＜0，a＞0可以推出对称轴x=-$\frac{b}{2a}$＞0，由c＞0可以得到此函数交y轴正半轴，由此即可确定它的图象经过的象限．
解答 解：∵a＞0，
∴开口方向向上，
∵b＜0，a＞0，
∴对称轴x=-$\frac{b}{2a}$＞0，
∵c＞0，
∴此函数交y轴正半轴．
∴它的图象经过一，二，四象限．
故选A．
点评 此题主要考查了二次函数图象与系数的关系，注意应用数形结合思想．
练习册系列答案
名校课堂系列答案
相关题目
如图，线段AB=8cm，C是AB的中点．D是AC的中点，则DB=6cm．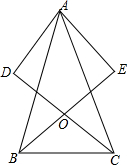
如图所示，下列四个条件，请你以其中三个为已知条件，第三个作为结论，推出一个正确的命题．（只需写出一种情况）
3．
如图，下列条件不能判断l1∥l2的是（ ）
如图，下列条件不能判断l1∥l2的是（ ）| A． | 180°-∠4=∠2 | B． | ∠1=∠3 | C． | ∠4=∠5 | D． | ∠2+∠4=180° |
张师傅要将一张残缺的圆形轮片恢复原貌（如图），已知轮片的一条弦AB的垂直平分线交弧AB于点C，交弦AB于点D，测得AB=24cm，CD=8cm．