题目内容
已知：如图，梯形ABCD中，AD∥BC，AB=DC，对角线AC、BD相交于点F，点E是边BC延长线上一点，且∠CDE=∠ABD．（1）求证：四边形ACED是平行四边形；
（2）连接AE，交BD于点G，求证：
| DG |
| GB |
| DF |
| DB |
考点：相似三角形的判定与性质,全等三角形的判定与性质,平行四边形的判定
专题：证明题
分析：（1）证△BAD≌△CDA，推出∠ABD=∠ACD=∠CDE，推出AC∥DE即可；
（2）根据平行得出比例式，再根据比例式的性质进行变形，即可得出答案．
（2）根据平行得出比例式，再根据比例式的性质进行变形，即可得出答案．
解答：证明：（1）∵梯形ABCD，AD∥BC，AB=CD，
∴∠BAD=∠CDA，
在△BAD和△CDA中
∴△BAD≌△CDA（SAS），
∴∠ABD=∠ACD，
∵∠CDE=∠ABD，
∴∠ACD=∠CDE，
∴AC∥DE，
∵AD∥CE，
∴四边形ACED是平行四边形；
（2）∵AD∥BC，
∴
=
，
=
，
∴
=
，
∵平行四边形ACED，AD=CE，
∴
=
，
∴
=
，
∴
=
，
∴
=
．
∴∠BAD=∠CDA，
在△BAD和△CDA中
|
∴△BAD≌△CDA（SAS），
∴∠ABD=∠ACD，
∵∠CDE=∠ABD，
∴∠ACD=∠CDE，
∴AC∥DE，
∵AD∥CE，
∴四边形ACED是平行四边形；
（2）∵AD∥BC，
∴
| AD |
| BE |
| DG |
| GB |
| BC |
| AD |
| BF |
| DF |
∴
| BC+AD |
| AD |
| BF+DF |
| DF |
∵平行四边形ACED，AD=CE，
∴
| BC+CE |
| AD |
| BF+DF |
| DF |
∴
| BE |
| AD |
| BD |
| DF |
∴
| AD |
| BE |
| DF |
| BD |
∴
| DG |
| GB |
| DF |
| DB |
点评：本题考查了比例的性质，平行四边形的判定，平行线的判定的应用，主要考查学生运用定理进行推理的能力，题目比较好，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
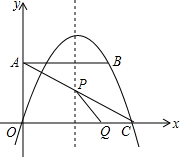如图，平面直角坐标系中，四边形OABC是直角梯形，AB∥OC，OA=5，AB=10，OC=12，抛物线y=ax2+bx经过点B、C．
给出定义，若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．