题目内容
一次函数y=kx+b的图象如图所示，则不等式0＜kx+b≤5的解集为考点：一次函数与一元一次不等式
专题：数形结合
分析：观察函数图象，函数图象与坐标轴两交点之间的部分满足0＜kx+b≤5，所以写出这个部分所对应的自变量的取值范围即可．
解答：解：观察函数图象得，当0≤x＜2时，0＜kx+b≤5，
所以不等式0＜kx+b≤5的解集为0≤x＜2．
故答案为0≤x＜2．
所以不等式0＜kx+b≤5的解集为0≤x＜2．
故答案为0≤x＜2．
点评：本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
发散思维新课堂系列答案
相关题目
对于任意整数n，多项式（n+7）2-（n-3）2的值都能（ ）
| A、被20整除 |
| B、被7整除 |
| C、被21整除 |
| D、被n+4整除 |
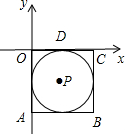如图，在平面直角坐标xOy中，边长为2的正方形OABC的顶点A、C，分别在y轴负半轴和x轴正半轴上，顶点B在第四象限，圆P与正方形边都相切，与x轴切点为D，在⊙P上有一动点Q使得三角形ODQ为等腰三角形，请写出△OAC区域内所有符合条件的点Q的坐标