题目内容
如图所示,AD∥BC,梯形ABCD的面积是180,E是AB的中点,F是BC边上的点,且AF∥CD,AF分别交ED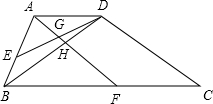 ,BD于G,H,设
,BD于G,H,设| BC | AD |
(1)若m=2,求△GHD的面积;
(2)若△GHD的面积为整数,求m的值.
分析:(1)若m=2,即BC=2AD,且四边形AFCD为平行四边形,可知F为BC中点,加上已知E为AB中点,可知G为△ABD的重心,从而求出AG和GH的比例关系,利用已知的总面积进而求出未知三角形在原图形中所占的比例,
(2)在(1)的基础之上,先求出△DHG面积,用m表示出来,进而考虑△DHG面积为整数时,m的取值.
(2)在(1)的基础之上,先求出△DHG面积,用m表示出来,进而考虑△DHG面积为整数时,m的取值.
解答:解:(1)∵AF∥CD,
∴四边形AFCD为平行四边形,
∴FC=AD=
BC,
∴F是BC的中点,
∴H为BD中点,
又∵E是AB的中点,故G为△ABD的重心,因此GH=
AG.(3分)
∴S△ABD=
SABCD=60,S△AHD=
S△ABD=30,S△GHD=
S△AHD=10.(6分)
(2)作BK∥AF交ED于K,
则△KEB≌△GEA,
∴AG=KB,
∴
=
=
=
=
=
.(9分)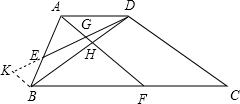
∴S△ABD:S△BCD=1:m,
∴S△ABD=
SABCD=
.S△AHD=
S△ABD=
,
S△GHD=
S△AHD=
.(12分)
即
为整数,因为180=22×32×5,所以m+1=2,3或6.
经验证,m+1=3或6,即m=2或5.(15分)
∴四边形AFCD为平行四边形,
∴FC=AD=
| 1 |
| 2 |
∴F是BC的中点,
∴H为BD中点,
又∵E是AB的中点,故G为△ABD的重心,因此GH=
| 1 |
| 2 |
∴S△ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)作BK∥AF交ED于K,
则△KEB≌△GEA,
∴AG=KB,
∴
| GH |
| AG |
| GH |
| KB |
| HD |
| BD |
| FC |
| BC |
| AD |
| BC |
| 1 |
| m |

∴S△ABD:S△BCD=1:m,
∴S△ABD=
| 1 |
| m+1 |
| 180 |
| m+1 |
| 1 |
| m |
| 180 |
| m(m+1) |
S△GHD=
| 1 |
| m+1 |
| 180 |
| m(m+1)2 |
即
| 180 |
| m(m+1)2 |
经验证,m+1=3或6,即m=2或5.(15分)
点评:解此题的关键是利用平行四边形的性质和重心的相关知识,来解决相关证明和计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
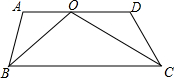 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC=
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC= 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒). 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒). 如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF.
如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF. 如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.
如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.