题目内容
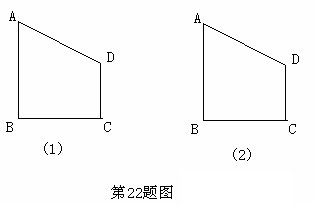
 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒).(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形ABQP是平行四边形?
(3)四边形ABQP能否为菱形?若能,求出t的值,若不能,说明理由.
(4)当t为何值时,以B,P,Q,三点为顶点的三角形是等腰三角形?
分析:(1)点P作PN⊥BC,垂足为N,则四边形PDCN为矩形,根据BQ=t,就得到S与t之间的函数关系式.
(2)当四边形ABQP为平行四边形时,PA=BQ,即t=21-2t,可将t求出;
(3)利用菱形性质得出当四边形ABQP为菱形,则AB=BQ=PA=PQ,得出边长之间关系即可得出答案;
(4)以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,②若BP=BQ,③若PB=PQ.在Rt△PMQ中根据勾股定理,就得到一个关于t的方程,就可以求出t.
(2)当四边形ABQP为平行四边形时,PA=BQ,即t=21-2t,可将t求出;
(3)利用菱形性质得出当四边形ABQP为菱形,则AB=BQ=PA=PQ,得出边长之间关系即可得出答案;
(4)以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,②若BP=BQ,③若PB=PQ.在Rt△PMQ中根据勾股定理,就得到一个关于t的方程,就可以求出t.
解答: 解:(1)如图1,过点P作PN⊥BC,于点N,
解:(1)如图1,过点P作PN⊥BC,于点N,
S=
×PN×BQ=
×12×t=6t,(0<t≤10.5);
(2)当四边形ABQP是平行四边形时,PA=BQ,
∴21-2t=t解得:t=7,
∴当t=7时,四边形ABQP是平行四边形.
(3)如图3,作BW⊥AD,于点W,AR⊥BC于点R,
当四边形ABQP为菱形,则AB=BQ=PA=PQ,
∵AB=
=
=13,
∴当AP=13,2t=21-13,t=4秒,此时BQ=4,
∴BQ≠AB,
∴四边形ABQP不能为菱形;

(4)①如图2,当BP=BQ时,由题意得:B(16,0),P(2t,12),Q(16-t,0),
∴BP=
=
,BQ=t,
PQ=
=
,
∴
=t,此时方程无实数根;
 ②图3,当BP=PQ时,PW=16-2t,PB=
②图3,当BP=PQ时,PW=16-2t,PB=
,
∴
=
,
解得:t1=
,t2=0,
但当t=0时,B,Q两点重合,故t=
;
③当BQ=PQ时,
=t,此时方程无实数根;
综上所述,当t=
秒时,以B,P,Q三点为顶点的三角形是等腰三角形;
 解:(1)如图1,过点P作PN⊥BC,于点N,
解:(1)如图1,过点P作PN⊥BC,于点N,S=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当四边形ABQP是平行四边形时,PA=BQ,
∴21-2t=t解得:t=7,
∴当t=7时,四边形ABQP是平行四边形.
(3)如图3,作BW⊥AD,于点W,AR⊥BC于点R,
当四边形ABQP为菱形,则AB=BQ=PA=PQ,
∵AB=
| AR2+BR2 |
| 122+52 |
∴当AP=13,2t=21-13,t=4秒,此时BQ=4,
∴BQ≠AB,
∴四边形ABQP不能为菱形;

(4)①如图2,当BP=BQ时,由题意得:B(16,0),P(2t,12),Q(16-t,0),
∴BP=
| BW2+PW2 |
| (2t-16)2+144 |
PQ=
| PN2+QN2 |
| (3t-16)2+144 |
∴
| (2t-16)2+144 |
 ②图3,当BP=PQ时,PW=16-2t,PB=
②图3,当BP=PQ时,PW=16-2t,PB=| (16-2t) 2+144 |
∴
| (16-2t) 2+144 |
| (3t-16)2+144 |
解得:t1=
| 32 |
| 5 |
但当t=0时,B,Q两点重合,故t=
| 32 |
| 5 |
③当BQ=PQ时,
| (3t-16)2+144 |
综上所述,当t=
| 32 |
| 5 |
点评:此题主要考查了二次函数的综合应用以及直角梯形的问题,通过作高线可以转化为直角三角形与矩形的问题.并且要理解以B、P、Q三点为顶点的三角形是等腰三角形,应分①若PQ=BQ,②若BP=BQ,③若PB=PQ.三种情况进行讨论是解题关键.

练习册系列答案
相关题目
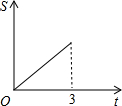
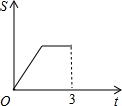
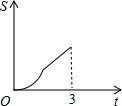
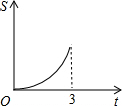
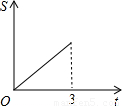
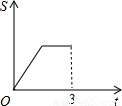
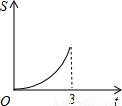
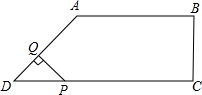 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )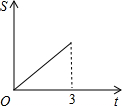
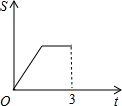
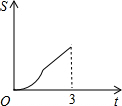
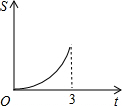

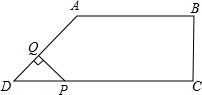 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是