题目内容
 如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF.
如图所示,AD∥BC,DCG是一条直线,∠1=∠2,∠3=∠4.求证:DE∥CF.分析:首先根据平行线的性质可得∠CDA=∠GCB,再由条件∠1=∠2,∠3=∠4可得∠2=
∠CDA,∠4=
∠GCB,进而得到∠2=∠4,再根据同位角相等,两直线平行判定出DE∥CF.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AD∥BC,
∴∠CDA=∠GCB,
∵∠1=∠2,
∴∠2=
∠CDA,
∵∠3=∠4,
∴∠4=
∠GCB,
∴∠2=∠4,
∴DE∥CF.
∴∠CDA=∠GCB,
∵∠1=∠2,
∴∠2=
| 1 |
| 2 |
∵∠3=∠4,
∴∠4=
| 1 |
| 2 |
∴∠2=∠4,
∴DE∥CF.
点评:此题主要考查了平行线的性质与判定,平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
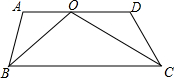 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC=
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC= 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点Q随之停止运动.设运动时间为t(秒). 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒). 如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.
如图所示,AD∥BC,∠BAD=∠BCD,那么直线AB与CD平行吗?请说明理由.