题目内容
 直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒).
直角梯形ABCD在直角坐标系中的位置如图所示,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点B出发,在线段BC上以每秒1个单位长的速度向点C运动,点P、Q分别从点D、B同时出发,当点P运动到与点A重合时,点P随之停止运动.设运动时间为t(秒).(1)求AB的长;
(2)设△BPQ的面积为S,求S与t之间的函数关系式;
(3)当t为何值时,四边形ABQP是平行四边形?
分析:(1)根据已知构造矩形,再利用矩形性质以及勾股定理求出AB即可;
(2)点P作PN⊥BC,垂足为N,则四边形PDCN为矩形,根据BQ=t,就得到S与t之间的函数关系式.
(3)当四边形ABQP为平行四边形时,PA=BQ,即t=21-2t,可将t求出;
(2)点P作PN⊥BC,垂足为N,则四边形PDCN为矩形,根据BQ=t,就得到S与t之间的函数关系式.
(3)当四边形ABQP为平行四边形时,PA=BQ,即t=21-2t,可将t求出;
解答: 解:(1)过点A作AE⊥x轴于点E,
解:(1)过点A作AE⊥x轴于点E,
∵AD∥BC,∠DCB=90°,
∴∠ADC=90°,
又∵∠AEC=90°,
∴四边形ADCE是矩形,
∵BC=16,DC=12,AD=21,
∴BE=AD-BC=5,AE=CD=12,
∴AB=
=13;
(2)如图,过点P作PN⊥BC,于点N,
S△BPQ=
×PN×BQ=
×12×t=6t,(0<t≤10.5);
(3)当四边形ABQP是平行四边形时,PA=BQ,
∴21-2t=t,
解得:t=7,
故当t=7时,四边形ABQP是平行四边形.
 解:(1)过点A作AE⊥x轴于点E,
解:(1)过点A作AE⊥x轴于点E,∵AD∥BC,∠DCB=90°,
∴∠ADC=90°,
又∵∠AEC=90°,
∴四边形ADCE是矩形,
∵BC=16,DC=12,AD=21,
∴BE=AD-BC=5,AE=CD=12,
∴AB=
| 52+122 |
(2)如图,过点P作PN⊥BC,于点N,
S△BPQ=
| 1 |
| 2 |
| 1 |
| 2 |
(3)当四边形ABQP是平行四边形时,PA=BQ,
∴21-2t=t,
解得:t=7,
故当t=7时,四边形ABQP是平行四边形.
点评:此题主要考查了勾股定理以及平行四边形的性质和矩形的性质以及三角形的面积等知识,通过作高线可以转化为直角三角形与矩形的问题是解题关键.

练习册系列答案
相关题目
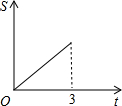
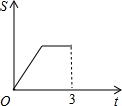
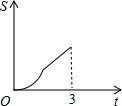
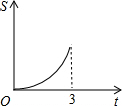
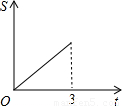
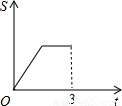
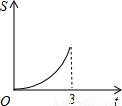
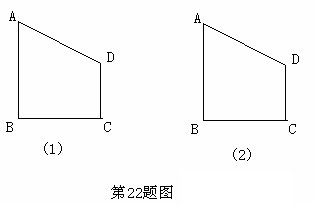
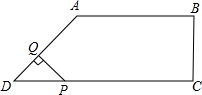 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )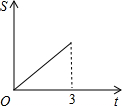
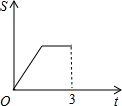
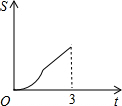
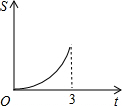

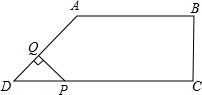 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是