题目内容
在Rt△ABC中，∠C=90°，∠B=45°，c=10，则a的长为（ ）
| A、5 | ||
B、
| ||
C、5
| ||
D、
|
考点：等腰直角三角形
专题：
分析：根据已知条件易推知Rt△ABC是等腰直角三角形，则a=b，所以根据勾股定理来求线段a的长度即可．
解答：
解：如图，∵在Rt△ABC中，∠C=90°，∠B=45°，
∴∠B=∠A=45°，
∴a=b，
∵c2=a2+b2，c=10，
∴2a2=100
解得a=5
．
故选：C．
解：如图，∵在Rt△ABC中，∠C=90°，∠B=45°，∴∠B=∠A=45°，
∴a=b，
∵c2=a2+b2，c=10，
∴2a2=100
解得a=5
| 2 |
故选：C．
点评：本题考查了等腰直角三角形的判定与性质．解题时，也可以通过解直角三角形来求线段BC的长度．
练习册系列答案
相关题目
若直线y=mx+2与y=nx-3的交点在x轴上，则
的值为（ ）
| m |
| n |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
点P在x轴的下侧，y轴的左侧，距离每个坐标轴都是3个单位长度，则点P的坐标为（ ）
| A、（3，3） |
| B、（-3，3） |
| C、（-3，-3） |
| D、（3，-3） |
函数y=4x-2与y=-4x-2的交点坐标为（ ）
| A、（-2，0） |
| B、（0，-2） |
| C、（0，2） |
| D、（2，0） |
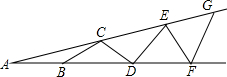如图，AB=BC=CD=DE=EF=FG，则∠A的范围是（ ）| A、0°＜∠A＜15° |
| B、0°＜∠A＜18° |
| C、0°＜∠A＜20° |
| D、0°＜∠A＜22.5° |
在坡度为1：7的斜坡上，一个人从A点出发向上运动到点B，若AB=30m，则此人升高了（ ）m．A、
| ||
B、
| ||
C、21
| ||
D、3
|
如图为不完整的正方体平面展开图，需补上一块，请画出两种情况．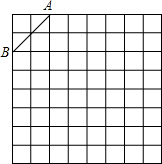
如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：