题目内容
6.已知关于x的一元二次方程(2m+1)x2+4mx+2m-3=0有两个不相等的实数根,则m的取值范围为:m>-$\frac{3}{4}$且m≠-$\frac{1}{2}$.分析 根据方程有两个不相等的实数根结合根的判别式以及二次项系数不为0,即可得出关于m的一元一次不等式组,解不等式组即可得出结论/
解答 解:∵关于x的一元二次方程(2m+1)x2+4mx+2m-3=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{2m+1≠0}\\{△=(4m)^{2}-4×(2m+1)×(2m-3)>0}\end{array}\right.$,
解得:m>-$\frac{3}{4}$且m≠-$\frac{1}{2}$.
故答案为:m>-$\frac{3}{4}$且m≠-$\frac{1}{2}$.
点评 本题考查了根的判别式,根据方程解的个数结合二次项系数不为0得出关于m的一元一次不等式组是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
18.将抛物线y=6x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线解析式是( )
| A. | y=6(x-2)2+3 | B. | y=6(x+2)2+3 | C. | y=6(x-2)2-3 | D. | y=6(x+2)2-3 |
15.若x2=4,则x=( )
| A. | ±2 | B. | 2 | C. | 4 | D. | 16 |
16.已知a,b,c 为有理数,并且a+b+c>0且abc<0,则a,b,c中负数有( )个.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
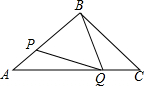 如图,在△ABC中,BA=BC=8cm,AC=10cm,点P从点A出发沿AB以每秒1cm的速度向点B运动,同时点Q从点C出发沿CA以每秒2cm的速度向点A运动,设运动时间为x秒,问:
如图,在△ABC中,BA=BC=8cm,AC=10cm,点P从点A出发沿AB以每秒1cm的速度向点B运动,同时点Q从点C出发沿CA以每秒2cm的速度向点A运动,设运动时间为x秒,问: 如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE.
如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE.