题目内容
18.阅读理解:已知直线l1的函数表达式为y=k1x+b1(k1≠0,k1,b1为常数),直线l2的函数表达式为y=k2x+b2(k2≠0,k2,b2为常数),若l1⊥l2,则有k1•k2=-1.
问题解决:
(1)已知直线y=4x+1与直线y=kx-1垂直,求k的值;
(2)若直线l经过A(-2,-5),且与y=-$\frac{1}{3}$x+3垂直,求直线l的表达式.
分析 (1)依据若l1⊥l2,则有k1•k2=-1,列方程求解即可;
(2)设l的解析式为y=3x+b,将点A的坐标代入求解即可.
解答 解:(1)∵直线y=4x+1与直线y=kx-1垂直,
∴4k=-1,解得:k=-$\frac{1}{4}$.
(2)∵直线l与y=-$\frac{1}{3}$x+3垂直,
∴设直线l的表达式为y=3x+b.
将A(-2,-5)代入得:-5=3×(-2)+b,解得b=1,
∴直线l的表达式为y=3x+1.
点评 本题主要考查的是两条直线相交于平行线问题,由若l1⊥l2,则有k1•k2=-1得到所求直线的一次项系数是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 180 | 185 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
10.某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
| 年 度 | 2013 | 2014 | 2015 | 2016 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).
7.下列方程中,是二元一次方程的为( )
| A. | 2x-3y=xy | B. | 3x+2=0 | C. | 2x=y2+1 | D. | 2x=3y |
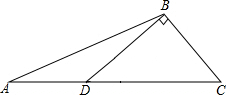 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)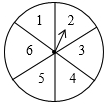 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜. 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.