Question

．如图，A、B、C、P是⊙O上的四个点，∠ACB=60°，且PC平分∠APB，则△ABC的形状是(     )

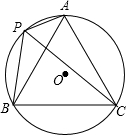
A．直角三角形     B．等腰三角形

C．等边三角形     D．等腰直角三角形

Answer 1

C【考点】圆周角定理；等边三角形的判定．

【分析】由圆内接四边形的性质得到∠APB=120°，根据角平分线的性质得到∠BPC=∠APC=60°，根据圆周角定理得到∠BAC=∠ABC=60°，即可得到结论．

【解答】解：∵A、B、C、P是⊙O上的四个点，∠ACB=60°，

∴∠APB=120°，

∵PC平分∠APB，

∴∠BPC=∠APC=60°，

∵∠BPC=∠BAC，∠APC=∠ABC，

∴∠BAC=∠ABC=60°，

∵∠ACB=60°，

∴△ABC为等边三角形．

故选C．

【点评】本题主要考查圆周角定理及等边三角形的判定，掌握在同圆或等圆中同弧所对的圆周角相等是解题的关键．