题目内容
【题目】已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.
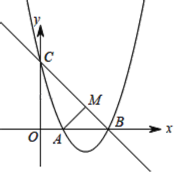

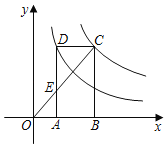
(1)求抛物线的解析式及顶点D的坐标;
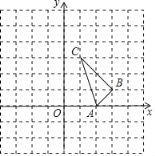
(2)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;
(3)若点Q为线段OC上的一动点,问:AQ+![]() QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3,则顶点D(2,﹣1);(2)P(![]() ,﹣
,﹣![]() );(3)H
);(3)H ,而点A(1,0),则AH=
,而点A(1,0),则AH=![]() ,即:AQ+
,即:AQ+![]() QC的最小值为
QC的最小值为![]() .
.
【解析】
将坐标(1,0),B(3,0)代入计算即可得出抛物线的解析式,即可计算出D的坐标.
将点B、C的坐标代入一次函数表达式计算,设点P(x,x2﹣4x+3),则点H(x,﹣x+3),求出x的值即可.
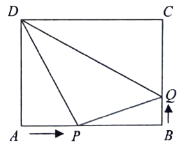
(3)存在,过点C作与y轴夹角为30°的直线CH,过点A作AH⊥CH,垂足为H,
则HQ=![]() CQ,Q+
CQ,Q+![]() QC最小值=AQ+HQ=AH,求出k值,再将A的坐标代入计算即可解答.
QC最小值=AQ+HQ=AH,求出k值,再将A的坐标代入计算即可解答.
(1)函数的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),即:3a=3,解得:a=1,
故抛物线的表达式为:y=x2﹣4x+3,则顶点D(2,﹣1);
(2)将点B、C的坐标代入一次函数表达式:y=mx+n并解得:
直线BC的表达式为:y=﹣x+3,过点P作y轴的平行线交BC于点H,
设点P(x,x2﹣4x+3),则点H(x,﹣x+3),
则S△PBC=![]() PH×OB=
PH×OB=![]() (﹣x+3﹣x2+4x﹣3)=
(﹣x+3﹣x2+4x﹣3)=![]() (﹣x2+3x),
(﹣x2+3x),
∵﹣![]() <0,故S△PBC有最大值,此时x=
<0,故S△PBC有最大值,此时x=![]() ,故点P(
,故点P(![]() ,﹣
,﹣![]() );
);
(3)存在,理由:
如上图,过点C作与y轴夹角为30°的直线CH,过点A作AH⊥CH,垂足为H,
则HQ=![]() CQ,Q+
CQ,Q+![]() QC最小值=AQ+HQ=AH,
QC最小值=AQ+HQ=AH,
直线HC所在表达式中的k值为![]() ,直线HC的表达式为:y=
,直线HC的表达式为:y=![]() x+3…①
x+3…①
则直线AH所在表达式中的k值为﹣![]() ,
,
则直线AH的表达式为:y=﹣![]() x+s,将点A的坐标代入上式并解得:
x+s,将点A的坐标代入上式并解得:
则直线AH的表达式为:y=﹣![]() x+
x+![]() …②,
…②,
联立①②并解得:x=![]() ,
,

故点H(![]() ,
,![]() ),而点A(1,0),则AH=
),而点A(1,0),则AH=![]() ,即:AQ+
,即:AQ+![]() QC的最小值为
QC的最小值为![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案