Question

【题目】在平面直角坐标系中，已知A（2，0）、B（3，1）、C（1，3）．

（1）画出△ABC沿x轴负方向平移2个单位后得到的△A1B1C1，并写出B1的坐标　 　；

（2）以A1点为旋转中心，将△A1B1C1逆时针方向旋转90°得△A1B2C2，画出△A1B2C2，并写出C2的坐标　 　；

（3）直接写出过B、B1、C2三点的圆的圆心坐标为　 　．

Answer 1

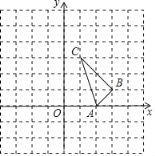
【答案】（1）（1，1）；（2）（﹣3，﹣1）；（3）（2，﹣6）．

【解析】

（1）根据平移变换的定义和性质作图可得；
（2）根据旋转变换的定义和性质作图可得；
（3）作B1C2和BB1的中垂线，交点即为所求点.

解：（1）如图所示，△A1B1C1即为所求，其中B1的坐标为（1，1），

故答案为：（1，1）；

（2）如图所示，△A1B2C2即为所求，其中C2的坐标为（﹣3，﹣1），

故答案为：（﹣3，﹣1）．

（3）如图所示，过B、B1、C2三点的圆的圆心P的坐标为（2，﹣6），

故答案为：（2，﹣6）．