Question

【题目】如图，点P（1，2），⊙P经过原点O，交y轴正半轴于点A，点B在⊙P上，∠BAO＝45°，则点B的坐标是_____．

Answer 1

【答案】(3,1)或(1,3)．

【解析】

作辅助线，先利用勾股定理求圆P的半径为，根据已知中的∠BAO=45°可知，两个满足条件的点B的连线就是圆P的直径，由此证明△BOG≌△BOH，设B（x，y），则OG=x，BG=y，从而列方程组可求出x、y的值，写出符合条件的点B的坐标．

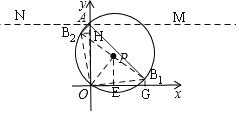
连接OP，过P作PE⊥x轴于E，

∵P(1,2)，

∴OE=1，PE=2，

由勾股定理得：OP=

过A作MN⊥x轴,分别作∠MAO、∠NAO的平分线交P于B、B，

则∠BAO=45°,∠BAO=45°，

∴∠BAB=90°，

连接BB,则BB是P的直径，即过点P，

∴BB=，

∴∠BOB=90°，

∵∠OBB=∠BAO=45°，

∴△BBO是等腰直角三角形，

∴OB=OB==，

过B作BG⊥x轴于G,过B作B2H⊥y轴于H，

∴∠OGB=∠OHB=90°，

∵∠GOB+∠AOB=90°,∠BOH+∠AOB=90°，

∴∠GOB=∠BOH，

∴△BOG≌△BOH，

∴BG=BH，OG=OH，

设B (x,y),则OG=x,BG=y，

∵∠BAO=45°，

∴△ABH是等腰直角三角形，

∴BH=AH=BG=y，

∴AO=AH+OH=x+y=4，

则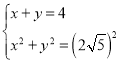

解得：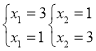

∵PB=，

∴x=1，y=3不符合题意，舍去，

∴B (3,1),B (1,3)，

则点B的坐标为(3,1)或(1,3)，

故答案为：(3,1)或(1,3).