Question

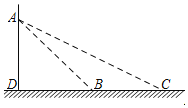
【题目】如图，在矩形中，cm，cm，点从点出发沿 以2cm/s的速度向终点匀速运动，同时点从点出发沿以1 cm/s的速度向终点匀速运动，、中有一点到达终点时，另一点随之停止运动.

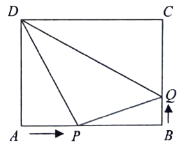
(1)几秒后，点、D的距离是点、的距离的2倍;

(2)几秒后，PDQ是直角三角形;

(3)在运动过程中，经过 秒，以为圆心，为半径的⊙与对角线相切.

Answer 1

【答案】（1）；（2）或11-；（3）.

【解析】

（1）设t秒后点P、D的距离是点P、Q距离的2倍，即PD=2PQ，根据勾股定理得，，利用，列方程：，即可解得t的值

(2)设t秒后，△DPQ是直角三角形分两种情况进行讨论：当∠DPQ=90°时，可证

△ADP △BPQ，利用 列方程即可求出t的值；当∠DQP=90°时，可证

△CDQ △BQP，利用 列方程即可求出t的值.

（3）连接BD，设⊙P与BD相切于m，连接PM，可知AP=PM=2t，BP=8-2t，

可得，在，列出方程：，

即可求出t的值.

解：

(1)设t秒后点P、D的距离是点P、Q距离的2倍，即PD=2PQ，

∵四边形ABCD是矩形，

∴∠A=∠B=90°，

∴，，

∵，

∴，

解得；

∵，

∴.

（2）设t秒后，△DPQ是直角三角形，

当∠DPQ=90°时，∠ADP=∠BPQ，

∵∠A=∠B=90°，

∴△ADP △BPQ，

∴，

∴，

解得: （舍去），

当∠DQP=90°时，∠CDQ=∠BQP，

∵∠B=∠C=90°，

∴△CDQ △BQP，

∴，

∴，

解得: （舍去），

答:当运动时间为或11-秒时，△DPQ是直角三角形；

（3）连接BD，设⊙P与BD相切于m，连接PM，

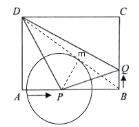
∴AP=PM=2t，

∴BP=8-2t，

∵AD=6，AB=8，

∴BD=10，

∴，

在，

∴，

解得t=.

故答案为.