题目内容
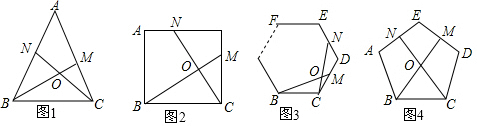
12.问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图1,在等边三角形ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN.
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
任务要求:
(1)请你从①、②两个命题中选择一个进行证明.
(2)请你继续完成下面的探索:
①如图3,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图4,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
分析 (1)①正三角形ABC中,可通过全等三角形来证明BM=CN,由于∠BON=∠MBC+∠BCO=60°,而∠ACB=∠ACN+∠OCB=60°,因此∠ACN=∠MBC,又知道∠A=∠BCM=60°,AC=BC,因此△ACN≌△CBM,可得出BM=CN;②同①;
(2)①由(1)的证明过程可知道∠MON的度数应该是正多边形的内角的度数,当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立,
②可参照(1)先得出三角形BCD和CDE全等,然后通过证三角形CEN和BDM全等来得出结论,在证三角形CEN和BDM全等的过程中也是通过∠BON与正五边形的内角相等得出一组对应角相等,然后根据正五边形的内角减去第一对全等三角形中得出的相等角来得出另一组对应角相等,可通过△BCD≌△CDE得出CE=BD,那么可得出三角形CEN和BDM全等,由此可得证.
解答 解:(1)选命题①
在图1中,∵△ABC是正三角形,
∴BC=CA,∠BCM=∠A=60°.
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
在△BCM和△CAN中,$\left\{\begin{array}{l}{∠BCM=∠A}&{\;}\\{BC=CA}&{\;}\\{∠CBM=∠ACN}&{\;}\end{array}\right.$,
∴△BCM≌△CAN(ASA).
∴BM=CN.
选命题②
在图2中∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠D=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
在△BCM和△CAN中,$\left\{\begin{array}{l}{∠BCM=∠D}&{\;}\\{BC=CD}&{\;}\\{∠CBM=∠DCN}&{\;}\end{array}\right.$,
∴△BCM≌△CDN(ASA).
∴BM=CN.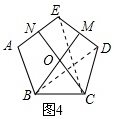
(2)①当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立.
②BM=CN成立.理由如下:
在图4中,连接BD、CE,
∵五边形ABCDE是正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,∠DEA=108°.
在△BCD和△CDE中,$\left\{\begin{array}{l}{BC=CD}&{\;}\\{∠BCD=∠CDE}&{\;}\\{CD=DE}&{\;}\end{array}\right.$,
∴△BCD≌△CDE(SAS).
∴BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵∠BON=108°,
∴∠OBC+∠OCB=108°.
∵∠OCB+∠OCD=108°,
∴∠OBC=∠OCD(即∠MBC=∠NCD).
∴∠MBC-∠DBC=∠NCD-∠ECD,即∠DBM=∠ECN.
∴∠CDE-∠BDC=∠DEA-∠CED,即∠BDM=∠CEN.
在△BDM和△CEN中,$\left\{\begin{array}{l}{∠BDM=∠CEN}&{\;}\\{BD=CE}&{\;}\\{∠DBM=∠ECN}&{\;}\end{array}\right.$,
∴△BDM≌△CEN(ASA).
∴BM=CN.
点评 本题是四边形综合题目,考查了等边三角形的性质,正方形的性质,全等三角形的判定与性质,正多边形等几何知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案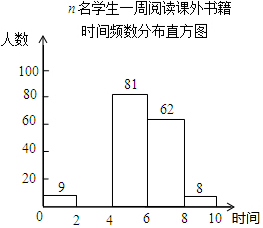 某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.n名学生一周阅读课外书籍时间频数分布表
| 时间段 | 频数 |
| 0<t≤2 | 9 |
| 2<t≤4 | 40 |
| 4<t≤6 | 81 |
| 6<t≤8 | 62 |
| 8<t≤10 | 8 |
(2)这组数据的中位数落在频数分布表中的哪个时间段?
(3)根据上述调查结果,估计该校2400名学生中一周阅读课外书籍时间在6小时以上的人数.
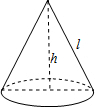 如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )| A. | 60π | B. | 65π | C. | 78π | D. | 156π |
| A. | |a|+|b| | B. | |a|-|b| | C. | |a+b| | D. | |a-b| |
