题目内容
18.在△ABC中,a,b,c为∠A,∠B,∠C的对边,已知a=2$\sqrt{3}$,b=6,∠A=30°,求∠ACB、∠ABC、和c.分析 根据在△ABC中,a,b,c为∠A,∠B,∠C的对边,已知a=2$\sqrt{3}$,b=6,∠A=30°,可以判断该三角形为直角三角形,从而可以解答本题.
解答 解:∵在△ABC中,a,b,c为∠A,∠B,∠C的对边,已知a=2$\sqrt{3}$,b=6,∠A=30°,
∴$\frac{a}{b}=\frac{2\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$,tan30°=$\frac{\sqrt{3}}{3}$=tanA,
∴此三角形为直角三角形,∠ACB=90°.
∴∠ABC=90°-30°=60°.
∴c=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{(2\sqrt{3})^{2}+{6}^{2}}=\sqrt{48}$=$4\sqrt{3}$.
即∠ACB=90°,∠ABC=60°,c=4$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是能根据已知条件判断该三角形为直角三角形.

练习册系列答案
相关题目
2.某地电话拨号人网有A、B两种计费方式.用户可任选其一;A为计时制:3元/小时;B为包月制;48元/月(限一部个人住宅电话人网).此外,每-种计费方式都得加收通讯费1.2元/时.
(1)按两种计费方式.把每月上网5小时、10小时、15小时、20小时、25小时的费用求出来,填入下表.
(2)当用户上网多少小时两种计费方式所交费用相同?
(3)由此可推测什么情况下选择计时制较划算?什么情况下选择包月制较划算?
(1)按两种计费方式.把每月上网5小时、10小时、15小时、20小时、25小时的费用求出来,填入下表.
| 时间(小时) | 5 | 10 | 15 | 20 | 25 |
| 计时制的费用(元) | 21 | 42 | 63 | 84 | 105 |
| 包月制的费用(元) | 54 | 60 | 66 | 72 | 78 |
(3)由此可推测什么情况下选择计时制较划算?什么情况下选择包月制较划算?
7.抛物线y=-2(x-4)2+5的开口方向、对称轴、顶点坐标分别是( )
| A. | 向下、直线x=-4、(4,5) | B. | 向上、直线x=-4、(-4,5) | ||
| C. | 向下、直线x=4、(4,5) | D. | 向上、直线x=4、(-4,-5) |
8.a、b是有理数,若ab>0,a+b>0,那么a、b的符号是( )
| A. | +,+ | B. | -,- | C. | +,- | D. | -,+ |
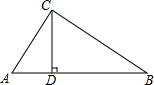 在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.
在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.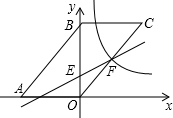 如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F. 若b是最小的正整数,且a、b满足(c-5)2+|a+b|=0.
若b是最小的正整数,且a、b满足(c-5)2+|a+b|=0.