题目内容
 如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP-AP|最大.
考点:圆的综合题
专题:几何综合题,压轴题
分析:(1)利用A,B点坐标得出AO,BO的长,进而得出AB的长,即可得出圆的半径;
(2)根据A,B 两点求出直线AB表达式为:y=-
x+3,根据 B,D 两点求出 BD 表达式为 y=
x+3,进而得出BD⊥AB,求出BD为⊙M的切线;
(3)根据D,O两点求出直线DO表达式为 y=
x 又在直线 DO 上的点P的横坐标为2,所以 p(2,
),此时|DP-AP|=DO=
.
(2)根据A,B 两点求出直线AB表达式为:y=-
| 3 |
| 4 |
| 4 |
| 3 |
(3)根据D,O两点求出直线DO表达式为 y=
| 5 |
| 6 |
| 5 |
| 3 |
| 61 |
解答:(1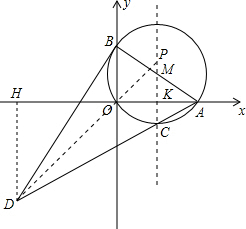 )解:∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,
)解:∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,
∴AB=5,
∴圆的半径为
;
(2)证明:由题意可得出:M(2,
)
又∵C为劣弧AO的中点,由垂径定理且 MC=
,故 C(2,-1)
过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 K,
则△ACK∽△ADH,
又∵DC=4AC,
故 DH=5KC=5,HA=5KA=10,
∴D(-6,-5)
设直线AB表达式为:y=ax+b,
,
解得:
故直线AB表达式为:y=-
x+3,
同理可得:根据B,D两点求出BD的表达式为y=
x+3,
∵kAB×kBD=-1,
∴BD⊥AB,BD为⊙M的切线;
(3)解:取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,
此P点为所求,且线段DO的长为|DP-AP|的最大值;
设直线DO表达式为 y=kx,
∴-5=-6k,
解得:k=
,
∴直线DO表达式为 y=
x
又∵在直线DO上的点P的横坐标为2,y=
,
∴P(2,
),
此时|DP-AP|=DO=
=
.
 )解:∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,
)解:∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,∴AB=5,
∴圆的半径为
| 5 |
| 2 |
(2)证明:由题意可得出:M(2,
| 3 |
| 2 |
又∵C为劣弧AO的中点,由垂径定理且 MC=
| 5 |
| 2 |
过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 K,
则△ACK∽△ADH,
又∵DC=4AC,
故 DH=5KC=5,HA=5KA=10,
∴D(-6,-5)
设直线AB表达式为:y=ax+b,
|
解得:
|
故直线AB表达式为:y=-
| 3 |
| 4 |
同理可得:根据B,D两点求出BD的表达式为y=
| 4 |
| 3 |
∵kAB×kBD=-1,
∴BD⊥AB,BD为⊙M的切线;
(3)解:取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,
此P点为所求,且线段DO的长为|DP-AP|的最大值;
设直线DO表达式为 y=kx,
∴-5=-6k,
解得:k=
| 5 |
| 6 |
∴直线DO表达式为 y=
| 5 |
| 6 |
又∵在直线DO上的点P的横坐标为2,y=
| 5 |
| 3 |
∴P(2,
| 5 |
| 3 |
此时|DP-AP|=DO=
| 62+52 |
| 61 |
点评:此题主要考查了勾股定理以及待定系数法求一次函数解析式以及两直线垂直系数的关系等知识,得出直线DO,AB,BD的解析式是解题关键.

练习册系列答案
相关题目
下面合并同类项正确的是( )
| A、2a+3b=5ab |
| B、2pq-4pq=-2pq |
| C、4m3-m3=3 |
| D、-7x2y+2x2y=-9x2y |

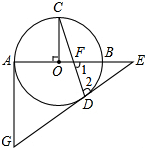 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E. (1)如图1,点C在线段AB上,线段AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(1)如图1,点C在线段AB上,线段AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度;