题目内容
如图,在平面直角坐标系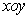 中,⊙A与y轴相切于点
中,⊙A与y轴相切于点 ,与x轴相交于M、N两点.如果点M的坐标为
,与x轴相交于M、N两点.如果点M的坐标为 ,求点N的坐标.
,求点N的坐标.

解:连接AB、AM,过点A作AC⊥MN于点C.
∵⊙A与y轴相切于点B(0, ),
),
 ∴AB⊥y轴.
∴AB⊥y轴.
又∵AC⊥MN,x 轴⊥y轴,
∴四边形BOCA为矩形.
∴AC=OB= ,OC=BA.
,OC=BA.
∵AC⊥MN,
∴∠ACM= 90°,MC=CN.
∵M( ,0),
,0),
∴OM= .
.
在 Rt△AMC中,设AM=r.
根据勾股定理得: .
.
即 ,求得r=
,求得r= .
.
∴⊙A的半径为 .
.
即AM=CO=AB = .
.
∴MC=CN=2 .
∴N( , 0) .
, 0) .

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
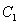 与经过点A、D、B的抛物线的一部分
与经过点A、D、B的抛物线的一部分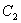 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,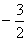 ),点M是抛物线
),点M是抛物线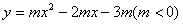 的顶点.
的顶点. ”在第四象限上是否存在一点P,使得
”在第四象限上是否存在一点P,使得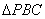 的面积最大?若存在,求出
的面积最大?若存在,求出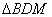 为直角三角形时,直接写出m的值.______
为直角三角形时,直接写出m的值.______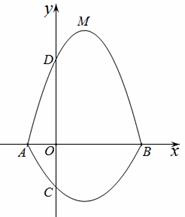
 的图象开口向上,并且经过原点
的图象开口向上,并且经过原点
 .
.
 的值;
的值; 测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是
测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是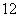 米 B.
米 B.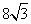 米 C.
米 C. 米 D.
米 D.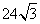 米 x k b 1 . c o m
米 x k b 1 . c o m
 .
.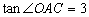 ,求抛物线的表达式;
,求抛物线的表达式; 相离、相切、相交.
相离、相切、相交.
 △ABC中,∠A=60°,AC2= AB2+AB.BC.
△ABC中,∠A=60°,AC2= AB2+AB.BC.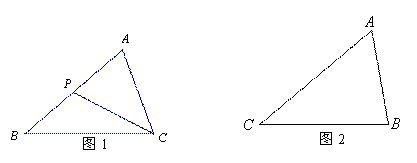 求∠B的度数.
求∠B的度数.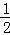 x2﹣
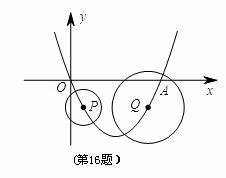
x2﹣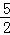 x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)
x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)