题目内容
锐角 中,
中, ,
, ,两动点
,两动点 分别在边
分别在边 上滑动,且
上滑动,且 ,以
,以 为边向下作正方形
为边向下作正方形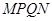 ,设其边长为
,设其边长为 ,正方形
,正方形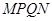 与
与 公共部分的面积为
公共部分的面积为 .
.
(1) 中边
中边 上高
上高 ;
;
(2)当 时,
时, 恰好落在边
恰好落在边 上(如图1);
上(如图1);
(3)当 在
在 外部时(如图2),求
外部时(如图2),求 关于
关于 的函数关系式(注明
的函数关系式(注明 的取值范围),并求出
的取值范围),并求出 为何值时
为何值时 最大,最大值是多少?
最大,最大值是多少? 
(1)AD=4;
(2)x=2.4;
(3)y=﹣ (x﹣3)2+6.当x=3时,y有最大值,最大值是6.
(x﹣3)2+6.当x=3时,y有最大值,最大值是6.
解析试题分析:(1)利用矩形的性质和相似三角形的性质,根据MN∥BC,得△AMN∽△ABC,求出△ABC中边BC上高AD的长度.
(2)因为正方形的位置在变化,但是△AMN∽△ABC没有改变,利用相似三角形对应边上高的比等于相似比,得出等量关系,代入解析式,
(3)用含x的式子表示矩形MEFN边长,从而求出面积的表达式.
试题解析:(1)由BC=6,S△ABC=12,得AD=4;
(2)当PQ恰好落在边BC上时,
∵MN∥BC,∴△AMN∽△ABC.
∴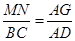 ,
,
即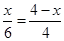 ,x=2.4;
,x=2.4;
(3)设BC分别交MP,NQ于E,F,则四边形MEFN为矩形.
设ME=NF=h,AD交MN于G(如图2)GD=NF=h,AG=4﹣h.
∵MN∥BC,
∴△AMN∽△ABC.
∴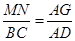 ,即
,即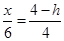 ,
,
∴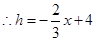 .
.
∴y=MN•NF=x(﹣ x+4)=﹣
x+4)=﹣ x2+4x(2.4<x<6),
x2+4x(2.4<x<6),
配方得:y=﹣ (x﹣3)2+6.
(x﹣3)2+6.
∴当x=3时,y有最大值,最大值是6.
考点:1.二次函数综合题2.矩形的性质.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目


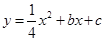 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC. 的值;
的值; 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与
 ,A(3,0),D(-1,0),E(0,3).
,A(3,0),D(-1,0),E(0,3).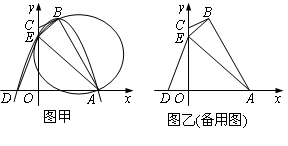
 ,
,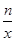 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;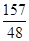 ,试求出t的取值范围.
,试求出t的取值范围. x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ; (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
